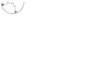What is the Angular Frequency of Small Oscillations for This System?

[peripatein]

Hi,

Homework Statement

I was given the setup in the attachment and was asked to find the angular frequency of small oscillations around the equilibrium. m1=m; m2=√3m

Homework Equations

The Attempt at a Solution

I have found L = 1/2*(3+√3)*mR²$\dot{θ}$² + mgRcosθ+√3mgRsinθ
and the point of equilibrium to be at tgθ=m2/m2=√3
Do I now substitute cosθ≈1-1/2$\dot{θ}$² and sinθ≈θ
and then write down Euler-Lagrange?

 

[haruspex]

Do I now substitute cosθ≈1-1/2$\dot{θ}$² and sinθ≈θ

The approximation you're thinking of is cosθ≈1-1/2$\θ$² for small θ. It's not with a $\dot{θ}$ in it, and it's not for what may be not a very small θ.
If θ is defined by tanθ=m2/m2=√3, you want to consider a small perturbation dθ from there. Try putting θ+dθ in your torque equation.

 

[peripatein]

I am not using any torque equations. I found the Lagrangian and was now thinking of using the Euler-Lagrange relation. In any case, could it be that k=second partial derivative of potential at point of equilibrium=2mgR
and hence angular frequency is sqrt(k/m)=sqrt(2gR)?

 

[peripatein]

Wait, dimensional analysis indicates I am wrong, doesn't it?

 

[peripatein]

I'd appreciate your feedback on the following attempt:
V = -mgR(cosθ + √3sinθ) ≈ -mgR(1 - 0.5θ² + √3θ)
First, is that the correct approach?
Second, do I now subsitute my θ of equilibrium in ∂²V/∂q² to get k in ω²=k/m?
Third, how do I find m in ω²=k/m? Is it by substituting my θ of equilibrium in the approximation -mgR(1 - 0.5θ² + √3θ)?

 

[haruspex]

I'd appreciate your feedback on the following attempt:
V = -mgR(cosθ + √3sinθ) ≈ -mgR(1 - 0.5θ² + √3θ)
First, is that the correct approach?

No, you didn't understand what I wrote before.
θ cannot be assumed to be small, so you cannot use those approximations. Find the equilibrium value of θ, then express θ as that value plus a small perturbation angle. Then you can use approximations for trig functions of the small perturbation.