What is the angular momentum of the clay-rod system?

[hidemi]

Homework Statement

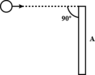
A thin rod of mass M and length L is struck at one end by a ball of clay of mass m, moving with speed v as shown in figure. The ball sticks to the rod. After the collision, the angular momentum of the clay-rod system about A, the midpoint of the rod, is

a. (m + M/3)(vL/2)
b. (m + M/12)(vL/2)
c. (m + M/6)(vL/2)
d. mvL/2
e. mvL

Answer: D

Relevant Equations

Angular Momentum = I W

I calculate in this way :
Angular Momentum = I W
= [ ( 1/12 ML^2 + m(L/2)^2 ] (V/ L/2)
= [ 1/12 ML^2 + 1/4 mL^2 ] 2V/L
= 2VL/4 [ M/3 + M]

but can not find a matching answer. Why?

 

[Delta2]

Not sure where your mistake is (I think it is that you take it to be that $W=\frac{V}{\frac{L}{2}}$, tell us how do you arrive at this conclusion), but you can find the answer very easy by using conservation of angular momentum.
What is the angular momentum of the system (around the midpoint A) at the time exactly before the collision?

 

[haruspex]

I'm not sure how to interpret "the angular momentum of the clay-rod system about A, the midpoint of the rod". From the answer given, it seems they mean the angular momentum about a fixed point in space where the midpoint of the rod was at impact. But that is not the same as the angular momentum about the midpoint of the rod as it moves just after impact. The latter would be slightly less, as it would exclude a component of m's angular momentum corresponding to the linear motion of the rod's mass centre.

I could not follow your reasoning. To figure out the velocities after impact, the conservation of angular momentum of the system is one of the equations you must start with.

 

[hidemi]

If use the conservation of energy, then it would look like this:

Li = Lf
mv = [1/12ML^2 + mL^2/4] * (v'/L)

As it is asking the angular momentum, so I just calculated the way I did in post #1.
I don't know how to continue further down.

 

[PeroK]

If use the conservation of energy, then it would look like this:

Li = Lf
mv = [1/12ML^2 + mL^2/4] * (v'/L)

As it is asking the angular momentum, so I just calculated the way I did in post #1.
I don't know how to continue further down.

Energy is not conserved but angular momentum is conserved.

 

[Frigus]

Angular momentum is not changing before and after Collision.
So I just calculated the ball's angular momentum before the collision and that will be the answer.
I think the mistake in your solution is that you are assuming velocity before and after the collision to be same.

 

[hidemi]

Thank you for all the discussions.
I understand the concept of conservation.
What I was confused previously was that when the collision happens, an angular momentum is applied to the rod which is in equilibrium, not moving or rotating at all initially. The ball sticks to the rod after collision, both of them rotate together and thus they generate an angular momentum, so I consider the I (inertia) includes both the rod and the ball which sticks at the end, that gives me the inertia [ 1/12 ML^2 + 1/4 mL^2 ].

Without considering the rod, the inertia would simply be 1/4 mL^2, which would then yields the given answer.

This was my thinking, in which we don't actually need to even think about the rod but solely the ball itself. Let me know if my thoughts are ok?

 

[PeroK]

Thank you for all the discussions.
I understand the concept of conservation.
What I was confused previously was that when the collision happens, an angular momentum is applied to the rod which is in equilibrium, not moving or rotating at all initially. The ball sticks to the rod after collision, both of them rotate together and thus they generate an angular momentum, so I consider the I (inertia) includes both the rod and the ball which sticks at the end, that gives me the inertia [ 1/12 ML^2 + 1/4 mL^2 ].

Without considering the rod, the inertia would simply be 1/4 mL^2, which would then yields the given answer.

This was my thinking, in which we don't actually need to even think about the rod but solely the ball itself. Let me know if my thoughts are ok?

You have to think about the rod. You're not thinking about what conservation actually means.

 

[Steve4Physics]

@hidemi, no calculation is needed to solve this problem. Just the basic definition of angular momentum and use of the law of conservation of angular momentum.

Angular momentum is initially taught to students as a property of a spinning/rotating mass. But an object moving in a straight line has angular momentum with respect to a given point.

Have you met $\vec L = \vec r \times \vec p$ or (simpler) $L = mvrsin\theta$ or (simplest) $L=mvr$? Check your notes/text-book!

Question: using only the definition of angular momentum, state the angular momentum of the moving clay with respect to rod’s centre before the collision? Problem solved!

 

[haruspex]

If use the conservation of energy, then it would look like this:
Li = Lf
mv = [1/12ML^2 + mL^2/4] * (v'/L)

How is that conservation of energy? The LHS is linear momentum, the RHS is angular momentum.
You have not defined v', but no obvious definition makes v'/L the angular velocity of the system.

Angular Momentum = I W
= [ ( 1/12 ML^2 + m(L/2)^2 ] (V/ L/2)

How do you get v/(L/2) for the angular velocity of the system after impact? That's the angular velocity of the clay about A before impact.

In short, you need to use conservation of angular momentum to find the angular velocity after impact, and since the question asks for the angular momentum, applying conservation gives you the answer immediately.

But I still say the question is misleading, as mentioned in post #3. I would have read it as asking for the angular momentum in the frame of reference of the rod's centre just after impact.

 

[hidemi]

How is that conservation of energy? The LHS is linear momentum, the RHS is angular momentum.
You have not defined v', but no obvious definition makes v'/L the angular velocity of the system.

How do you get v/(L/2) for the angular velocity of the system after impact? That's the angular velocity of the clay about A before impact.

In short, you need to use conservation of angular momentum to find the angular velocity after impact, and since the question asks for the angular momentum, applying conservation gives you the answer immediately.

But I still say the question is misleading, as mentioned in post #3. I would have read it as asking for the angular momentum in the frame of reference of the rod's centre just after impact.

(V/(L/2)) is from w=V/r = v/(L/r)
I wonder if this is correct?

 

[haruspex]

(V/(L/2)) is from w=V/r = v/(L/r)
I wonder if this is correct?

In post #1 you calculated w=v/(L/2) and used that as though it is the angular velocity of the system just after impact. But v is the linear velocity of the ball of clay before impact, so you have calculated the angular velocity of the system as though (i) the clay mass continues with unchanged velocity and (ii) the velocity of the rod's centre just after impact is still zero.

 

[hidemi]

In post #1 you calculated w=v/(L/2) and used that as though it is the angular velocity of the system just after impact. But v is the linear velocity of the ball of clay before impact, so you have calculated the angular velocity of the system as though (i) the clay mass continues with unchanged velocity and (ii) the velocity of the rod's centre just after impact is still zero.

Thank you so much. I got it.