mathmari
Gold Member
MHB
- 4,984
- 7
Hey! 
Using Gauss theorem I want to calculate $\iint_{\Sigma}f\cdot NdA$, where $\Sigma$ is the closed boundary surface of the pyramid with vertices $(0,0,0), (1,0,0), (0,1,0), (0,0,1), (1,1,0)$ and $f(x,y,z)=(x^2y, 3y^2z, 9xz^2)$ and the perpendicular vectors $N$ to the inside of the pyramid.
From Gauss theorem we have that $$ \iint_{\Sigma}f\cdot N \ dA=\iiint_{\Omega}\nabla\cdot f \ dV$$ We have that $$\nabla \cdot f=\frac{\partial{(x^2y)}}{\partial{x}}+\frac{\partial{(3y^2z)}}{\partial{y}}+\frac{\partial{(9xz^2)}}{\partial{z}}=2xy+6yz+18xz$$
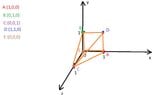
Now we have to find the boundaries for the integral. We have the pyramid
View attachment 7634
So, do we have to find the equation of each line segment of the pyramid? (Wondering)
Using Gauss theorem I want to calculate $\iint_{\Sigma}f\cdot NdA$, where $\Sigma$ is the closed boundary surface of the pyramid with vertices $(0,0,0), (1,0,0), (0,1,0), (0,0,1), (1,1,0)$ and $f(x,y,z)=(x^2y, 3y^2z, 9xz^2)$ and the perpendicular vectors $N$ to the inside of the pyramid.
From Gauss theorem we have that $$ \iint_{\Sigma}f\cdot N \ dA=\iiint_{\Omega}\nabla\cdot f \ dV$$ We have that $$\nabla \cdot f=\frac{\partial{(x^2y)}}{\partial{x}}+\frac{\partial{(3y^2z)}}{\partial{y}}+\frac{\partial{(9xz^2)}}{\partial{z}}=2xy+6yz+18xz$$
Now we have to find the boundaries for the integral. We have the pyramid
View attachment 7634
So, do we have to find the equation of each line segment of the pyramid? (Wondering)