karush
Gold Member
MHB
- 3,240
- 5
\begin{align*}\displaystyle
R&= y=0 \quad y=2x+4 \quad y=x^3\\
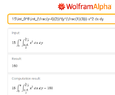
A&=\iint\limits_{R}15x^2\, dA\\
&=\int_{0}^{8} \int_{{(y-4)}/2}^{y^{1/3}} 15x^2\,dx \\
&=\int_{0}^{8}\biggr[5x^3\large\biggr]_{{(y-4)}/2}^{y^{1/3}}\quad dx\\
&=\int_{0}^{8}[5(y^{1/3})^3-5((y-4)/2))^3] \quad dx\\
&= ?
\end{align*}
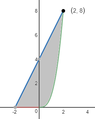
attempted plot
View attachment 7870
just seeing if I am going in the right direction with this
no book answer?
R&= y=0 \quad y=2x+4 \quad y=x^3\\
A&=\iint\limits_{R}15x^2\, dA\\
&=\int_{0}^{8} \int_{{(y-4)}/2}^{y^{1/3}} 15x^2\,dx \\
&=\int_{0}^{8}\biggr[5x^3\large\biggr]_{{(y-4)}/2}^{y^{1/3}}\quad dx\\
&=\int_{0}^{8}[5(y^{1/3})^3-5((y-4)/2))^3] \quad dx\\
&= ?
\end{align*}
attempted plot
View attachment 7870
just seeing if I am going in the right direction with this
no book answer?