- #1
Boris Leykin
- 21
- 0
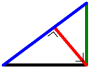
In a right-angled triangle hypotenuse equals 10, altitude equals 6. What is the area of the triangle?
Answers: 60, 30, 24, 16
Answers: 60, 30, 24, 16