mathdad
- 1,280
- 0
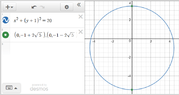
A. Determine the center and radius of circle.
B. Also, find the y-coordinates of the points (if any) where the circle intersects the y-axis.
View attachment 7462
B. Also, find the y-coordinates of the points (if any) where the circle intersects the y-axis.
View attachment 7462
Attachments
Last edited by a moderator: