What is the charge of each conductor afterwards?

[haruspex]

I was looking into the Uniqueness theorem in electrostatics, which says (I think) that if the potential of the connected conductors were known, the E field would everywhere be unique. And a unique E field implies unique surface charge.
The snag is that we have not shown that the potential of the connected conductors is the same irrespective of how contact is made. I suppose the prima facie belief is that it is not, that V varies with how contact is made.

I agree that the overall potential is likely to depend the configuration, but this is quite a different question, right? If it does depend on the configuration, it could still turn out that the two charges are equal, and even if it is independent of configuration the charge split could differ for the same potential.

Edit: As an indicator that the potential does depend on configuration, consider a large number of identical spheres. Arranged as a tight ball the potential would be more than when arranged as a spherical shell.
The same model says the charges will be different for different spheres in the tight ball.
Showing these results for two objects will be tougher.

 

[rude man]

If connecting two similar charged rods in two different ways always resulted in the same ensemble potential, then you could slide one rod against another without losing contact until you get the same juxtaposition for both connecting ways. Then by the uniqueness theorem the charge distributions would have to be the same since potential and juxtaposition would be the same. Unfortunately, I guess there would be two differing ensemble potentials so the Q distributions would also differ.

 

[haruspex]

If connecting two similar charged rods in two different ways always resulted in the same ensemble potential

Yes, but I think it's easy to see that it won't. Placed side by side would surely create a higher potential than end to end. Likewise a pair of plates.

 

[rude man]

Yes, but I think it's easy to see that it won't. Placed side by side would surely create a higher potential than end to end. Likewise a pair of plates.

Not obvious to me, but no argument either.

 

[haruspex]

Not obvious to me, but no argument either.

This paper, http://www.colorado.edu/physics/phys3320/phys3320_sp12/AJPPapers/AJP_E&MPapers_030612/Griffiths_ConductingNeedle.pdf, gives exact expressions for charge distribution in and equipotentials near an infinite thin ribbon. See section I
V.
It should be possible to compare two such ribbons placed edge to edge (doubling λ and a) with placing them face to face (doubling λ only).

 

[TSny]

Here's another example that I think supports the conjecture that the congruent conductors do not need to end up with equal charges.

Consider a thin-walled conical conductor

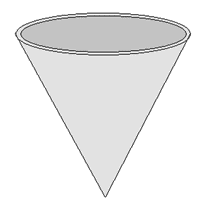
If you put charge on this, then I believe that most of the charge will be located on the outer surface. Very little charge will be on the inner surface, especially if the apex angle is small. But I don't know how to prove this.

Now slip an identically shaped, uncharged conductor inside of the charged one until they touch.

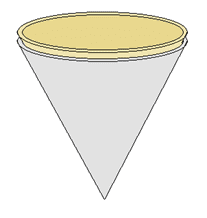
This is almost like a single conical conductor. So, most of the charge should remain on the outer surface of the outer conductor.

This example is not meant as a proof, but I think it is suggestive.