- #1
antigen123
- 5
- 0
Homework Statement
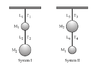
Image 1 Shows both system 1 and system 2 at rest
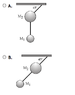
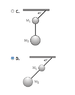
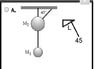
Images 2 and 3 show answer choices:
Given M2 > M1, which of the following pendulum systems has the GREATEST change in potential energy from a state of rest?
Passage says: The greatest Potential energy is always associated with the system whose center of mass is is displaced from its resting state.
Homework Equations
The Attempt at a Solution
I got the correct answer (D)by process of elimination. however I am still having trouble locating the center of mass just by observing an object(where would the center of mass be on this object?). I feel this is because of a lack of a solid conceptual understanding of what it is. Is the center of mass a point where net torque is zero and net force is zero??