What Is the Correct Angle Between Vectors a and c?

[nafisanazlee]

Homework Statement

Let a = 2i + j - 2k, b = i + j and c be a vector such that |c-a| = 3, | (a x b) x c| = 3 and the angle between c and a x b is 30°. Then, a.c is equal to?

Relevant Equations

a.b = |a||b|cosθ
|a×b| = |a||b|sinθ

The solution to the question is attached herewith. I approached in the exact same way and got |c| = 2. Then I thought like this:
the angle between a and a×b is 90°, and the angle between c and a×b is 30° (given). So one of the possibilities is, the angle between a and c is 90-30=60° degree. |a| = 3, and a.c gives me 2.3.cos60° = 3, which is not the correct answer. My question is, am I wrong in some way? Or the question has some problem in it?

 

[Delta2]

Can you provide us your detailed reasoning on why you think that the angle between a and c is 60 degrees?.

By the way you infer that it is 60 degrees it seems to me that you assume that the vectors a, axb and c are all belonging on the same plane but this is not the case. According to standard euclidean geometry two vectors always belong in the same plane, but three vectors dont always do that.

 

[Mark44]

Then I thought like this:
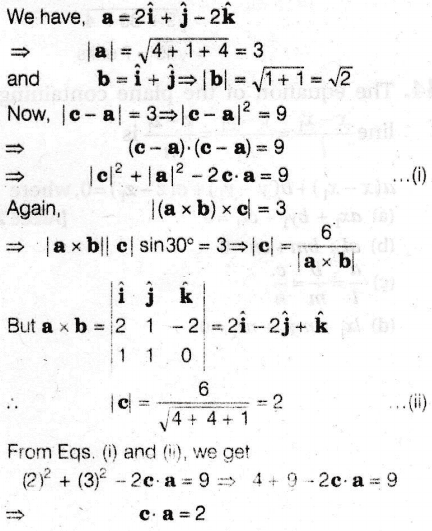
the angle between a and a×b is 90°, and the angle between c and a×b is 30° (given). So one of the possibilities is, the angle between a and c is 90-30=60° degree.

There's a flaw in your logic. The cross product a×b defines a vector that is perpendicular to the plane in which a and b lie. The fact that c makes an angle of 30° doesn't necessarily mean that c makes an angle of 60° with either a or b, only that it makes this angle with the plane that a and b lie in.

 

[nafisanazlee]

There's a flaw in your logic. The cross product a×b defines a vector that is perpendicular to the plane in which a and b lie. The fact that c makes an angle of 30° doesn't necessarily mean that c makes an angle of 60° with either a or b, only that it makes this angle with the plane that a and b lie in.

got it, thanks!

 

[nafisanazlee]

Can you provide us your detailed reasoning on why you think that the angle between a and c is 60 degrees?.

By the way you infer that it is 60 degrees it seems to me that you assume that the vectors a, axb and c are all belonging on the same plane but this is not the case. According to standard euclidean geometry two vectors always belong in the same plane, but three vectors dont always do that.

Thank you! got it.