What is the correct term for the bright point on the retina in imaging?

[John_H]

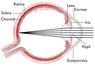
Here is a typical photo of imaging in the eye. The bright point on the retina is called out, in a book on the biology of vision, as the focal point. I am pretty sure the book is wrong, and that this is NOT the rear focal point. The rear focal point would be somewhere closer to the back surface of the lens -- not at the retina. Correct?

But I don't know what you would call this point on the retina. A bright point, but there must be a formal name for it.

Thank you for your insights.

John

 

[jtbell]

The diagram indicates that the object is at infinity, or practically infinity, as indicated by the incoming parallel rays. Therefore I would call that point on the retina the rear focal point for this system, that is, the lens with air on the incoming side and intraocular fluid on the outgoing side. If the lens had air on both sides, the light would focus at a different location, of course, and that would be the focal point for a system consisting of the lens with air on both sides.

 

[John_H]

Thank you for your help on this.

Your analysis makes excellent sense but if the focal point is that far back along the axis of the lens, then where should the image form?

Here are a couple of additional pictures. (I have collected several of these, trying to puzzle it out). In one illustration, there seems to be a tiny but perceptible divergence of the rays, just at the retina. This would make sense, because it would plant the image on the fovea, a tiny pit packed with cones. (Without the fovea we are blind).

In the other picture, the one imaging the eye chart, I can't make sense of what is happening. It seems as though a chart of that size could only be imaged on a screen somewhere deep behind they eyesocket.

I guess I would vote for the first picture, but the divergence of rays shown is so tiny it might be my imagination -- I guess I want one to be there, to be consistent with my own understanding, or misunderstanding, or how an image is formed.

Thank you again for your insights on this.

John

 

[jtbell]

It's not where the focal point is located, per se, it's where the image point is located, that matters. If the object is at infinity (or at least very far away), the image is at the focal length (or located very close to the focal length) away from the lens. If the object is close to the eye, then the focal point is somewhere inside the eyeball, and the image point is still at the retina.

Keep in mind is that the eye lens changes shape according to the tension of the muscles that surround it, thereby changing the focal length of the system. That's how we can focus on objects at varying distances without changing the image distance, which is fixed because the eyeball is in a bone socket. This is called accommodation. If you're looking at something clearly, then the image must be at the surface of the retina, or at least close enough that the blurring is small enough not to be noticeable.

Neither of your two most recent diagrams is an accurate ray diagram of the type you'd find (or should find!) in a physics book, by the way. The diagram in the earlier posting, is more accurate, at least for a pointlike object at infinity.

 

[John_H]

Still trying to hammer through to a clear understanding of this thing. Here is where I am.

It seems to me that most of the time, and for most objects, there has to be some finite distance between the focal point and the image point. The rays converging from the lens should crossover at the back focal point and then fan out, however slightly, to the image plane. Otherwise there would be no image – just a point.

http://micro.magnet.fsu.edu/primer/java/scienceopticsu/eyeball/index.html"

There is a nice animation, here, of imaging in the eye. It is not possible to shift the object (that is the butterfly) all the way out to infinity, but if we could, yes, it seems the image of the butterfly would collapse to a point.

From the thin lens equation, attached, we can also see that if the distance to the object really becomes infinite, the d-sub-o term collapses to zero, leaving an equation in which the distance to the focal point and the distance to the image point are indeed identical. This also makes physical sense, because you would expect the image of a distant star, for example, to be nothing more than a single tiny bright point.

But in the everyday world observed objects are not, in fact, infinitely far away. I would have to urge that in the everyday case, there must be some divergence of rays beyond the focal point of the lens in the eye -- in order to project a small image onto the plane of the retina. Put another way it seems to me that for worldly objects, the image plane needs to be a plane – it cannot be a point.

In my edition of Halliday & Resnick, most of the illustrations dwell on the more traditional high-low treatment of image formation, in which for example a candle standing upright on the optical axis well in front of the lens and is projected as an inverted image, suspended upside down from the optical axis in the image plane, well behind the lens.

There is just one centered and symmetrical illustration of rays arriving parallel to the centerline of a converging lens. No object, no image. They do show rays diverging from the back focal point, but no image point or plane is discussed. They have nothing to say about it, except to note that the incoming rays are parallel, and converge to the back focal point.

If the focal point in the eye were positioned precisely at the surface of the retina, instead of slightly in front of the retina, then what the retina would “read” would not be an image. It would be something more like the Fourier transform of an image. If the object were a distant star, you might not notice the difference. If the object were across the street, however, it could be pretty freaky.

Regards, John

 

[OlderDan]

That butterfly illustration is somewhat instructive, but it is not really helping you with the issue of the focal point relative the the retina because the crossover point in that image is not the focal point. What it does show is that the lens has an adjustable focal point controlled by the eye muscles. The Haliday and Resnick type image can easily be extended to an object that has points on both sides of the axis. Just extend the base of the candle through the axis, and the image will be extended through the axis.

To form an image on the retina for an object not at infinity, the focal point does need to be in front of the retina. The Halidy and Resnick type diagram will show you exactly where the focal point must be to form the image on the retina. It is always close to the retina because the focal length is so short. For an object that is essentially at infinity (i.e., thousands of focal lengths away), the image is still not a point. The object still has size, and the image has size. Rays from one edge of the object arrive at a small angle relative to the axis and are brought into focus off-axis in the focal plane. Likewise for the rays from the other edge. The angle subtended by a pair of lines from the center of the lens to the edges of the object is exactly the same as the angle subtended by a pair of lines from the center of the lens to the edges of the image (in the thin lens apporximation). The image formed is an image in the focal plane, and the size of the image is the size of the object times the ratio of focal length to object distance. The Haliday and Resnick type diagram for the extended object (both sides of the axis) will show you very clearly these equal angles for an object at any distance from the lens.

 

[John_H]

Thank you for your help.

I sketched the Halliday & Resnick drawing and pulled lines as you have suggested. It basically seems to show that the centerline/symmetrical picture is the same in principle as the one usually presented, with objects and images arranged to stand on, or hang down from, the optical axis. So perhaps we could shift the discussion to this more conventional diagram, here.

http://micro.magnet.fsu.edu/primer/java/lenses/converginglenses/index.html"

As long as there is a distance, however small, between the focal plane and the image plane, I don't have any problems.

In the limit of the infinitely distant object, or the "essentially" infinitely distant object, I am still completely at a loss.

From the animation here, for example, it appears that as the object heads for the western horizon, the image shrinks and the image plane and the focal plane get closer and closer together, pretty much as predicted by the lens equation.

As we approach the limit, that is, the instant when the the focal plane and the image plane actually merge -- it looks like the rays traced from the points on the object to the corresponding points on the image are contracting to a point. We are only seeing rays from one pair of conjugate points, but I think this contraction would include all of the rays from all of the points you might select.

In other words I can easily see how an image forms in the image plane.

I can't seem to visualize how an image plane can back up into the focal plane. It still appears to me that when this happens, the image will collapse to a point.

Maybe it is a terminology problem.

Thank you again for your insights, this is very helpful.

John.

 

[OlderDan]

What do you say we play a trick on the animation. Since it will not let us move the object to the Western horizon, let's reverse the roles of the object and the image. As long as we are talking about real images, the roles are completely reversible. Change the name Object to Image' and the name Real Image to Object'. Now move the slider to move Object' as far as you want to the East. You will lose sight of Object', but you will still see the rays from its tip coming into the lens and coming to focus at Image'. When Image' is in the focal plane, the rays from the very tip of Object' are parallel and come to focus at the tip of Image'. The tail of Object' is still on the axis, and the rays from the tail (not shown) are coming to focus exactly at F. The rays from a point half way between the tip and tail of Object' are parallel and come to focus at a point half way between the tail and tip of Image'. The angle between the Principal Ray from the tip (shown) and the axis is unrelistically large in this diagram, but for a real distant object like the moon, with you looking at one edge, the principal ray from the other edge would be coming in at about a half degree angle to the axis. If you were looking at the center of the moon, the principal ray from each edge would be coming in at about one quarter degree to the axis. The important thing to note is that no matter how large the object, the angle between the axis and the principal ray is exactly the same both entering and exiting the lens. For an object essentially at infinity, all the rays from one point on the object are parallel and come to focus at one point, but each point on the object has its own set of parallel rays and each set comes to focus at a different point in the focal plane. By similar triangles, the ratio of Image' size to Object' size is exactly the same as the ratio of the Image' distance to Object' distance. (The image' distance equals the focal length for an object at ~infinity.) If the very distant object has extent, its image in the focal plane has extent.

 

[John_H]

Thank you for your counsel on this.

The scissoring of the optical axis and principal ray is very good. It is clear that if the object has extent, the image must also have extent. No question here.

It must be a problem with how words are used. The problem words are “focal plane” and “image plane.”

What do you call the plane where the image appears for an object “essentially at infinity”? Put another way, can you really say, formally and accurately, that this image forms on the focal plane?

If it is the convention to say the image forms on the focal plane (and apparently it is), but everybody already knows it actually forms on the image plane instead, and that the two planes are so close together the distinction is just a mathematical formality, then okay. I’ll just shutup and get in line.

But if an image with extent really does form on the focal plane, then I still don’t see how it happens, given the equations and diagrams we have been looking at here.

For objects which are not “essentially at infinity,” there exist two distinctly separate and different planes behind the lens, the focal plane and the image plane. The image appears on the image plane. I think everybody agrees on this.

As the object heads for infinity, the two planes get closer and closer together. But they cannot merge until the object actually reaches infinity. Which is to say, they never merge. This means, in the practical terms specified by the lens equation, that there always exists a distinction, a physical gap, however tiny, between the focal plane and image plane.

I seem to be insisting that the image always forms on the image plane, and never on the focal plane. If we said that for an object positioned “essentially at infinity” the image appears “essentially at the focal plane” or “very close to the focal plane,” then I am okay. But it seems to me the image never “snaps”, in the sense of a CAD program, to the focal plane.

In the purely theoretical case where the object is infinitely distant, and the two planes do merge, I think the image collapses. In other words, how could I expect to see an infinitely distant object? Surely it would produce an infinitely small image?

If the object is positioned anywhere this side of infinity, yes, I can see that the image must have extent. But that image is formed on the image plane, not the focal plane. The lens equation requires this. As the object goes away the image plane approaches the focal plane, but it never gets there. Is this wrong?

In the reversal of the cartoon, if we redefine the object as an image, then the “image” clearly still has extent when it is sitting on the focal point, and the “object” has gone to southeastern infinity. But in the cartoon, the physical dimensions of the object, which we are now calling the “image” -- have been frozen solid by the programmer. The image should be free to contract and expand. I will have to think about this some more, but it seems to me that although the lens principle is freely reversible, the cartoon isn’t.

I think the distance and the distinction between the focal plane and the image plane becomes more clear in wave optics, where imaging is explained as a double diffraction process. The “double” has reference to diffraction effects at the two different planes, the back focal plane and the image plane. Probably why I am struggling to keep the two planes physically separated, except in the very special case of the infinitely distant object.

Thank you again for you insights. It helps to air this out.

Regards, John

 

[OlderDan]

You have it right. There will always be at least an infinitesimal separation between the focal plane and the image plane for any object in a plane, even one at a great distance from the lens. You are also correct that for any object that is truly "at infinity" the angle subtended by that object goes to zero. If W is the width of an object and d_o its distance from the lens, then the angle it subtends is θ = W/d_o which clearly goes to zero as d_o goes to infinity. So the image of such an object has to be a point.

But the world and physics are full of situations where it no longer makes sense to hold onto the infinitesimals in our analysis. If we did that, we would never be able to treat projectile motion as if the force on the projectie were a constant. It is not a constant. The force is inversely proportional to the square of the distance from the center of the earth, and when we throw an object in the air, it does have the horizontal and vertical components we say it has. There is an additional tangential component due to the Earth's rotation. The path it follows is not a parabola. It is an ellipse with the center of the Earth at a focus and points on the surface of the Earth travel in circular paths somewhere under this ellipse until the ellipse crosses paths with some surface point. It only looks parabolic to an observer on the Earth who is willing to ignore the finer details of the motion.

The same is true of the image of the lens. There is no such thing as an ideal thin lens that focuses light parallel to its axis at one precise focal point. The lens of the eye is not even a thin lens, and the retina is not a plane. There are few objects of interest to us that have all of their parts in a plane at one distance from the lens, yet we routinely form acceptable images of these 3 dimensional objects on flat film. Photographers are all familiar with the concept of "depth of field", the range of possible object distances that form images that appear "sharp enough" at one fixed image distance. Ignoring these effects is already an approximation that is a bigger problem than letting the image surface go to the focal surface in the limit of large object distances.

In the analysis of every problem there comes a time when good enough is good enough. Recognizing that in the limit as the object distance approaches infinity (nothing ever gets to infinity) the image plane merges with the focal plane (it never quite gets there) is just one manifestation of the game of "good enough" we all play every day.

 

[John_H]

Thank you again for your patience in working through this. I agree that it seems like a trivial distinction, but it is helpful to me, in trying to understand this, to establish that the focal plane does not contain an image; and that the focal plane and the image plane are two different things, except in the rare instant when an object goes infinitely far away.

Thanks again for your input on this. John