What Is the Correct Way to Calculate Theta in Trigonometry?

[r-soy]

Hi all


question on triangometry .

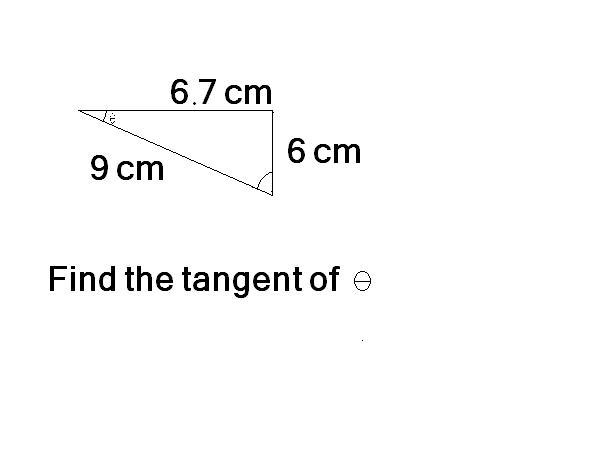
I know solve this quetion put are we saying :

tan = 6/6.7 = 0.8955

or tan =6/6.7 =0.0156

I don't n did we take tan or direct divide 6/6.7 = 0.8955

I want your help please .

 

[Borek]

TRIANGOMETRY?

What is tangent definition?

--

 

[r-soy]

thanks >> I understand now

 

[Borek]

[URL]http://www.bpp.com.pl/IMG/faint.gif[/URL]

 

[k-rod AP 2010]

you divide the opposite side/adjacent side to the angle θ, which is 6/6.7= 0.89.

Then you take the tangent of this number, tan(0.89) = .0156 as your final answer

 

[The legend]

[PLAIN]http://www.bpp.com.pl/IMG/faint.gif[/QUOTE]

hey ... where did you get it from?

EDIT: understood...

 

[Theaumasch]

you divide the opposite side/adjacent side to the angle θ, which is 6/6.7= 0.89.

Then you take the tangent of this number, tan(0.89) = .0156 as your final answer

No, the opposite side divided by the adjacent side already is the tangent of theta

 

[k-rod AP 2010]

No, the opposite side divided by the adjacent side already is the tangent of theta

ohh ur right, i meant to say you would take the arctangent to find out the theta. i forgot to hit arctangent on my calculator and just put the number w/o paying attention. my bad,