What is the Displacement Equation for a Wave?

[daveamal]

Homework Statement

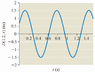
The time plot for a wave of wavelength 0.68 m, moving toward the right, is shown at x = 1.2 m in the figure below. (Assume the wave is a sine wave and that it is propagating to the right.)
(a) What is the angular frequency of the wave?
(b) What is the speed of the wave?
(c) What is the phase constant of the wave?
(d) Write a displacement equation for the wave. (Use the following as necessary: x and t. Assume SI units. Do not enter units in your expression.)

Homework Equations

ω(angular frequency)=(2\Pi)/T
k(wave number)=(2\Pi)/\lambda
\lambda=wavelength
D(x,t)=Acos(kx-ωt+\phi)
\phi=phase constant
v(speed)=ω/k

The Attempt at a Solution

I found angular frequency and speed by the given equations and got them as 9.38 rad/sec and 1 m/sec respectively. Then I found k by using the given wavelength and got 9.24 rad/meter and by plugging in values found the phase constant as -5. The amplitude is 1.5 m.

I am stuck at writing the displacement equation:
What I thought it would be was-
D(x,t)=1.5cos(9.24x-9.38t-5) but it's wrong. I even tried using sin instead of cos as it is a sin wave but it was still wrong.
I am really confused as for what will be the answer . Thanks for the help

 

[Simon Bridge]

in general:

D(x,t)=Asin(kx-wt+p)

w=angular frequency, p=phase offset.

I suspect you have misread the graph and/or missed an algebra step out.

You are given: D(1.2,t) = Asin(wt+q) ... the new phase factor q depends on x as well as p. q=(1.2)k+p
You are also supplied with the wavelength λ

You can get A right off the graph. You have A=1.5m - I agree.

Find q by putting t=0 and comparing with the graph. Do this.

Find k from the wavelength - well done: it is OK to express numbers as a multiple of pi.
So the wavelength is 68/100m, which makes k=50π/17 rad/m... you can stop there: it's the same as yours.

With q, k, and x, you can find p.

To find w you need the period T ... please show me this calculation step-by-step.

That should be everything.
I suspect it's the values for p and w where you made a mistake.
It does not matter if it is sine or cosine ... only the phase offset is different.

 

[daveamal]

Thanks! I found time period (T) by approximating from the graph, i.e (1.28-0.61) which is 0.67. Then I found ω by using the formula and got 9.38 rad/sec. Is that the correct way?

 

[daveamal]

For phase constant p, I found the D at around 0.15 m. Than as you said, I used 0.15=1.5sin(1.2κ-p) and got p as -5.4 which I rounded to -5. The web-assign says that both ω and p are correct. I don't know why I get the equation wrong.

 

[daveamal]

Oh, there was some problem with the web-assign question, so it was showing wrong. Thanks for the help though :D

 

[Simon Bridge]

OK good.
When that happens, it is hard to tell where the mistake lies - which is where being carefully systematic helps.

For comparison - I noticed that the sine wave passed through the t-axis at about 0.28-0.29, and then again at 1.28-1.29 ... 1.5 periods later. So I would have done: (1.5)T=1s so T=(2/3)s making w= 2π/T = 6π/2 = 3π rad/s

(notice that the pi looks a bit like an enn but you can sort of tell?)

At t=0, D=(3/4)m

Note: you have D=0.15m ... how did you get that?
I see that the first peak is at t=0.15s ...

... I avoid decimals if I can?
i.e. I'd write the amplitude as A=(3/2)m

From the formula:
D=Asin(q) ... so sin(q) = D/A = (3/4)(2/3) = 2/4 = 1/2

(recall q=kx+d - for x=(6/5)m) ... so what angle makes the sine 0.5?
it's from one of those special triangles that are good to memorize:

so q = π/6 = 6k/5 + d and you know that k=50π/17 ... job done.

The thing about this approach is that it is a lot easier to troubleshoot ... also, leaving the pi out like that, and keeping things in fractions, means you don't have to worry about accumulating rounding-off errors ;)

BTW: I think I misplaced a minus sign.

 

[daveamal]

Oh I see, this makes things simple. Thanks!

 

[Simon Bridge]

No worries - I don't normally do that much for someone but it looked like you had pretty much the lot.
The exercise is mostly about matching the equation with the graph - good for building understanding.

The other thing they like to do is give you a snapshot of the position wave at two times ... say D(x,t1) and D(x,t2) ... and you have to construct the equation from that.

Enjoy.