What is the Displacement of the Wedge When the Smaller Block Reaches the Bottom?

[utkarshakash]

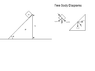
Homework Statement

Find the displacement of wedge when the smaller block reaches the bottom of wedge.

Homework Equations

See attached diagram.

The Attempt at a Solution

For the smaller block,
$N = mg \cos \theta \\ mg \sin \theta = m v \dfrac{dv}{dx}$

For wedge
$N \sin \theta = M v \dfrac{dv}{dx}$

Let the smaller block attain velocity v when it reaches the bottom and the velocity of wedge at that instant be v'.
Using conservation of energy,
$\dfrac{mv^2}{2} + mgh = \dfrac{Mv' ^2}{2}$

Solving the above three equations gives me the displacement of wedge as 2h/cosΘ sinΘ. But unfortunately this is not the correct answer. Can anyone help me figure out the mistake?

 

[haruspex]

Your equation for N is only correct if m has no acceleration in the direction normal to the wedge's surface. Since the wedge accelerates that need not be true.

 

[utkarshakash]

Your equation for N is only correct if m has no acceleration in the direction normal to the wedge's surface. Since the wedge accelerates that need not be true.

OK. Let's say the wedge has an acceleration a' at any time t. Thus, If I take the wedge as the reference frame, I'd have to include a pseudo force as well towards left. So the equation for smaller block then becomes

$N + ma' \sin \theta = mg \cos \theta \\ mg \sin \theta + ma' \cos \theta = m v \dfrac{dv}{dx}$

For the wedge, I can write

$N \sin \theta = M v' \frac{dv'}{dx}$

Since the block has two components of velocity when it reaches bottom viz. v' parallel to X-aixs and v parallel to inclined plane, the net velocity is $v_{net} ^2 = v^2 + v' ^2$

Now If I use energy conservation

$mgh = \dfrac{mv_{net} ^2}{2} + \dfrac{M v' ^2}{2}$

Solving the above equations, however, yield x = 0 !.

 

[Saitama]

OK. Let's say the wedge has an acceleration a' at any time t. Thus, If I take the wedge as the reference frame, I'd have to include a pseudo force as well towards left. So the equation for smaller block then becomes

$N + ma' \sin \theta = mg \cos \theta \\ mg \sin \theta + ma' \cos \theta = m v \dfrac{dv}{dx}$

For the wedge, I can write

$N \sin \theta = M v' \frac{dv'}{dx}$

These equations are sufficient, I don't see the need of writing a' as v'dv'/dx or a as vdv/dx. Can you solve the above equations to find a and a'?

 

[utkarshakash]

These equations are sufficient, I don't see the need of writing a' as v'dv'/dx or a as vdv/dx. Can you solve the above equations to find a and a'?

$a' = \dfrac{mg \cos \theta \sin \theta}{M+m \sin ^2 \theta} \\ a = g \sin \theta + \dfrac{mg \cos ^2 \theta \sin \theta}{M + m \sin ^2 \theta}$

But I need to find displacement and not acceleration.

 

[Saitama]

$a' = \dfrac{mg \cos \theta \sin \theta}{M+m \sin ^2 \theta} \\ a = g \sin \theta + \dfrac{mg \cos ^2 \theta \sin \theta}{M + m \sin ^2 \theta}$

But I need to find displacement and not acceleration.

I haven't checked if the above expressions are correct.

Now that you have the accelerations, can you find the time it take the block to reach the ground? You have to find the displacement of wedge corresponding to this time.

 

[Saitama]

Looks like we missed the easier approach.

The problem can be easily solved by conservation of linear momentum. :)

 

[utkarshakash]

I haven't checked if the above expressions are correct.

Now that you have the accelerations, can you find the time it take the block to reach the ground? You have to find the displacement of wedge corresponding to this time.

I get the answer as $\dfrac{mh \cot \theta}{M+m}$. But the correct answer is $\dfrac{mh}{M+m}$. In the meantime, I solved this problem using another method and got the same result.(the term that includes cotθ) So, I think there's a flaw in the solutions manual. But it'd be better if you could confirm my result.

 

[Saitama]

I get the answer as $\dfrac{mh \cot \theta}{M+m}$. But the correct answer is $\dfrac{mh}{M+m}$. In the meantime, I solved this problem using another method and got the same result.(the term that includes cotθ) So, I think there's a flaw in the solutions manual. But it'd be better if you could confirm my result.

I got the same answer as yours by both the methods. (Force and conservation of linear momentum) :)