Suvadip
- 68
- 0
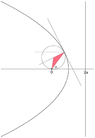
A circle is drawn through the focus of the parabola $2a/r=1+ \cos( \theta)$ to touch it at the point $\theta=\alpha$. Find the eq. of the circle in polar form.
Please help
Please help
Last edited by a moderator: