What is the equation of the circumcircle of triangle PAB?

[utkarshakash]

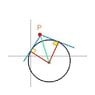
Homework Statement

Tangents drawn from a point P(2,3) to the circle $$x^2+y^2-8x+6y+1=0$$ touch the circle at the points A and B. Find equation of circumcircle of the ΔPAB.

The Attempt at a Solution

The chord of contact is equal to -x+3y+1=0. This is also the radical axis of the given circle and circumcircle. Let equation of circumcircle be S' and given circle be S.

Then S-S' = -x+3y+1

But the above equation does not seem to give the correct equation of circumcircle as it does not satisfy P.

 

[Saitama]

Then S-S' = -x+3y+1

This is definitely incorrect. There could be infinite solutions to S' sharing the same chord with S. Instead, try writing down the family of circles passing through the points of intersection of a given circle and a given chord i.e $S+\lambda L=0$. Plug in (2,3) to find a value for $\lambda$.

Btw, the circumcircle passes through centre of given circle. I don't see how to proof this but if somebody can prove this, then its a one or two line problem.

 

[ehild]

See picture. What are the yellow angles, the tangent lines make with the radii?

Remember Thales' Theorem and its converse http://en.wikipedia.org/wiki/Thales'_theorem

ehild

 

[Saitama]

See picture. What are the yellow angles, the tangent lines make with the radii?

Remember Thales' Theorem and its converse http://en.wikipedia.org/wiki/Thales'_theorem

ehild

Ah, that is so neat, thanks ehild!

 

[ehild]

You are welcome

ehild

 

[phinds]

Btw, the circumcircle passes through centre of given circle. I don't see how to proof this but if somebody can prove this, then its a one or two line problem.

I think I must be missing something here in the comments by Pranav-Arora and ehild. I interpret it that you are both saying that the if there is a circle that contains on its circumference the point P and the two points A and B, which are on the original circle at the point where a line from P is tangent to the original circle, thus making it a circumcircle of the chord ABP then that circle ALSO contains the center of the given circle as a point on its circumference? Is that how I should be interpreting what you are saying? I assume not, since it so clearly is not true but I can't figure out how else to interpret what you are saying.

 

[Saitama]

Is that how I should be interpreting what you are saying?

Yes, that's what we are saying. :)

I assume not, since it so clearly is not true but I can't figure out how else to interpret what you are saying.

Why not?

 

[ehild]

Remember Thales' Theorem. The converse of Thales' theorem states that a right triangle's hypotenuse is a diameter of its circumcircle. See the picture: there are two right triangles, with common hypotenuse. Are A, B, P and the centre of the given circle all on the same circle?
ehild

 

[phinds]

Damn. It is, isn't it. My bad, clearly. I thought that as the point approached the circle, the radius of the circumcircle would get smaller and smaller. Shows what my intuition is worth, huh?

 

[ehild]

Damn. It is, isn't it. My bad, clearly. I thought that as the point approached the circle, the radius of the circumcircle would get smaller and smaller. Shows what my intuition is worth, huh?

Yes it gets smaller and smaller but does not go down to zero ...


ehild

 

[phinds]

Yes it gets smaller and smaller but does not go down to zero ...


ehild

Yeah, as the distance from the point to the circle approaches zero the radius of the circumcircle in question approaches the radius of the original circle, not zero as I mistakenly intuited it.

 

[Saitama]

@utkarshakash: Do you see the one line solution? :)

 

[utkarshakash]

@utkarshakash: Do you see the one line solution? :)

Actually my book already contains that "one line solution" which states that P and the centre of circle are diametrically opposite points of the circumcircle. Initially you correctly pointed out that the centre of given circle will lie on the circumcircle but I was waiting for someone to explain why this is true and it seems like ehild did the job pretty well. Thanks to all of you :)

 

[phinds]

Yeah, as the distance from the point to the circle approaches zero the radius of the circumcircle in question approaches the radius of the original circle, not zero as I mistakenly intuited it.

Jeez ... I haven't gotten ANYTHING right in this. The above is a mis-statement. I meant (or should have meant) that the DIAMETER of the circumcircle approaches the radius of the original circle.

I think maybe I should give up math.

Or just keep my mouth shut.

Possibly both

 

[Saitama]

Actually my book already contains that "one line solution" which states that P and the centre of circle are diametrically opposite points of the circumcircle. Initially you correctly pointed out that the centre of given circle will lie on the circumcircle but I was waiting for someone to explain why this is true and it seems like ehild did the job pretty well. Thanks to all of you :)

Do you have more of these? You haven't posted a lot in Math section recently. :3

 

[utkarshakash]

Do you have more of these? You haven't posted a lot in Math section recently. :3

I know it's been a while since I posted in the Math section. It's because I already have the solutions to these problems and I can look them up whenever I want. It saves a lot of time.

btw, have a look at this thread

https://www.physicsforums.com/showthread.php?t=753528

 

[Saitama]

btw, have a look at this thread

https://www.physicsforums.com/showthread.php?t=753528

I already did but haven't been able to come up with any answer. Do you have a solution or final answer to this? I doubt the solution involves the method Ray Vickson has shown.

 

[utkarshakash]

I already did but haven't been able to come up with any answer. Do you have a solution or final answer to this? I doubt the solution involves the method Ray Vickson has shown.

I couldn't understand his method as well. I don't have the final answers either. So ultimately I left the question.

 

[sankalpmittal]

Quite late to post here.

Using one point form :

Tangent is y-3=m(x-2)

Now using perpendicular distance of this line from circle = Radius, you get two values of m. Consequently you can get points A and B by making the two equations identical to their point form one by one.

Then you get coordinates A and B.

Now I hope you can find the equation of circle through 3 points.