What is the Equivalent Resistance of an Infinite Circuit with 1 kΩ Resistors?

[Saitama]

Homework Statement

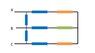
Determine the resultant resistance of the infinite circuit made up of $1 k\Omega$ resistors shown in the figure between points A and C, and between points A and B.

Homework Equations

The Attempt at a Solution

I can find the equivalent resistance between A and C. In this case, I can remove the middle branch of resistors originating from B but I am clueless about finding the equivalent between A and B, I can't see the repeating unit here.

Any help is appreciated. Thanks!

 

[phyzguy]

Try thinking of it this way. Suppose you just had an infinite network connected to A and B without the lower part connected to C, and call each resistor R. Then the resistance between A and B is just the parallel combination of R with (2R + Req), where Req is the equivalent resistance of the network on the right stretching off to infinity. But since the network is infinite, Req is equal to the resistance between A and B (because removing one leg of an infinite network leaves you with the same infinite network). So you can just set up an equation and solve for Req. Once you've conquered this technique, you should be able to apply it to the more complex case you are given.

 

[dauto]

Try thinking of it this way. Suppose you just had an infinite network connected to A and B without the lower part connected to C, and call each resistor R. Then the resistance between A and B is just the parallel combination of R with (2R + Req), where Req is the equivalent resistance of the network on the right stretching off to infinity. But since the network is infinite, Req is equal to the resistance between A and B (because removing one leg of an infinite network leaves you with the same infinite network). So you can just set up an equation and solve for Req. Once you've conquered this technique, you should be able to apply it to the more complex case you are given.

That doesn't seem to work in that case.

 

[dauto]

What you have to do is to replace the whole network with three resistors instead of one. The first resistor R_A connects the point A with an extra node - say D. the second resistor R_B connects the point B with D and the third resistor R_C, identical to R_A by symmetry, connects C with D. Then we have

A -------R_A------|

|​

B -------R_B------D

|​

C -------R_A------|

Replacing the infinite network.

Try that.

 

[phyzguy]

That doesn't seem to work in that case.

Yes, I see that now. This is more complicated than I thought. Hmmmm... But I don't see how your RA, RB solution works, either.

 

[dauto]

Yes, I see that now. This is more complicated than I thought. Hmmmm... But I don't see how your RA, RB solution works, either.

It works the same way that the usual method works. Replace part of the infinite network (a part identical to the whole network) with the tree resistors and compare that with the situation where the whole network was replaced with resistors

 

[dauto]

More ASCII art

A --------R_A------|

|​

B --------R_B------|

|​

C --------R_A------|

should be equivalent to

A ----------1Ω------R_A---|
...|.......|
...1Ω......|
...|.......|
B ----------1Ω------R_B---|
...|.......|
...1Ω......|
...|.......|
C ----------1Ω------R_A---|

 

[phyzguy]

Yes, I see now. You can then look at the resistance between A and B and at the resistance between A and C and get 2 equations in two unknowns to solve for RA and RB. The results are consistent with the simpler single network result. Pranav-Arora, do you see?

 

[Saitama]

More ASCII art

A --------R_A------|

|​

B --------R_B------|

|​

C --------R_A------|

should be equivalent to

A ----------1Ω------R_A---|
...|.......|
...1Ω......|
...|.......|
B ----------1Ω------R_B---|
...|.......|
...1Ω......|
...|.......|
C ----------1Ω------R_A---|

I am not sure if I understand the circuit you have drawn. I have attached my interpretation of your circuit, is it correct? If so, I don't see how you get that.

The blue ones are for $1k\Omega$, orange for$R_A$ and green for $R_B$.

 

[phyzguy]

What you have drawn is correct. What dauto is saying is that you can replace the infinite network with just those three resistors. The reasoning is as follows. If you measure the resistance between A and B, you will get some value, and by symmetry it will be the same as the resistance between B and C. Also, if you measure the resistance between A and C you will get some other value. So there are only two resistance values that characterize the network. So you can replace the entire network with just those three resistors. The resistance between A and B (equal to the resistance between B and C) is RA+RB, and the resistance between A and C is 2RA. Now we just have to determine RA and RB. We do this by shifting to the right one step, and replacing the (still infinite) network with those same three resistors. Then you can write two equations in two unknowns and solve for RA and RB.

 

[dauto]

phyzguy's answer above is correct. I just want to point out that the resistance R_B might turn out to be negative. That's no reason to worry since this is not a real resistance. It's just a device used to solve the problem. The real resistances are R_AB = R_A + R_B, and R_AC = 2R_A. These must be positive.

 

[Saitama]

Sorry for the delay in reply.

What you have drawn is correct. What dauto is saying is that you can replace the infinite network with just those three resistors. The reasoning is as follows. If you measure the resistance between A and B, you will get some value, and by symmetry it will be the same as the resistance between B and C. Also, if you measure the resistance between A and C you will get some other value. So there are only two resistance values that characterize the network. So you can replace the entire network with just those three resistors. The resistance between A and B (equal to the resistance between B and C) is RA+RB, and the resistance between A and C is 2RA. Now we just have to determine RA and RB. We do this by shifting to the right one step, and replacing the (still infinite) network with those same three resistors. Then you can write two equations in two unknowns and solve for RA and RB.

The equivalent resistance between A and B for the circuit I attached before is:
$$\frac{1}{R_{AB}}=1+\frac{1}{\frac{(R_A+2)(R_A+1)}{R_A+R_B+3}+R_A+1}$$
Also,
$$R_{AB}=R_A+R_B$$
$$R_{AC}=2R_A=\sqrt{5}-1\,k\Omega \Rightarrow R_A=\frac{\sqrt{5}-1}{2}$$
Solving does give me the right answer but I still don't understand why can you replace the infinite circuit with just three resistors.

 

[phyzguy]

Suppose you had a black box filled with resistors hooked up in some unknown way, and two wires coming out. Don't you see that if you connect an ohmmeter to the two wires you will measure some value of resistance? So you can replace the black box with a single resistor, no matter what is in the box. Now add a third wire. There are only three ways to hook it to the ohmmeter - A to B, A to C, and B to C, so there are only three resistances that characterize the whole black box.

 

[Saitama]

Suppose you had a black box filled with resistors hooked up in some unknown way, and two wires coming out. Don't you see that if you connect an ohmmeter to the two wires you will measure some value of resistance? So you can replace the black box with a single resistor, no matter what is in the box. Now add a third wire. There are only three ways to hook it to the ohmmeter - A to B, A to C, and B to C, so there are only three resistances that characterize the whole black box.

Yes, I agree about the ohmmeter part and that there are three way to connect it but how does that explain that the circuit can be reduced to only three resistors?

 

[dauto]

Yes, I agree about the ohmmeter part and that there are three way to connect it but how does that explain that the circuit can be reduced to only three resistors?

That's puzzling. You don't seem bothered at all by the replacement of a circuit by a single equivalent resistance between A and B, but seem bothered by the replacement of a circuit by thee resistors. It's the same principle. In general, a circuit with N external connection points may be replaced by an equivalent circuit with N(N-1)/2 resistors.

EDIT: what was the final answer after the math cleared up?

 

[haruspex]

You don't seem bothered at all by the replacement of a circuit by a single equivalent resistance between A and B, but seem bothered by the replacement of a circuit by thee resistors. It's the same principle. In general, a circuit with N external connection points may be replaced by an equivalent circuit with N(N-1)/2 resistors.

It's not obvious to me how this works for a system with N external contacts. Is there a theorem to this effect that you can point to?

 

[dauto]

I don't know the name of the theorem. But it is based on the superposition principle of linear systems. If the black box contains only ohmic components than the output (current for instance) is linearly related to the input (applied voltage) and the superposition of inputs (adding the inputs) leads to superposition of outputs. This forms a linear vector space where the vectors represent the possible conditions (input and output) of the system. The somewhat hard (though very intuitive) part of the theorem is to prove that the vector space has N(N-1) dimensions.

EDIT: Apparently one application of this theorem is called the "Star-mesh transform" while for the special case of three connecting points the "Star-mesh transform" is called the "Y - Δ" theorem.

 

[haruspex]

I don't know the name of the theorem. But it is based on the superposition principle of linear systems. If the black box contains only ohmic components than the output (current for instance) is linearly related to the input (applied voltage) and the superposition of inputs (adding the inputs) leads to superposition of outputs. This forms a linear vector space where the vectors represent the possible conditions (input and output) of the system. The somewhat hard (though very intuitive) part of the theorem is to prove that the vector space has N(N-1) dimensions.

Yes, I had managed to figure that much out, but it seemed you went further and were saying it could be reduced to the specific arrangement of one resistor between each pair of the N.

Apparently one application of this theorem is called the "Star-mesh transform" while for the special case of three connecting points the "Star-mesh transform" is called the "Y - Δ" theorem.

Again, I had managed the Y-Δ transformation, but to reduce an arbitrary network with three contacts to a Δ requires the general star-mesh transform. Looking at the Wikipedia entries, http://en.wikipedia.org/wiki/Star-mesh_transform and http://en.wikipedia.org/wiki/Schur_complement, this is far from trivial. Thanks for the clue.
Pranav-Arora was right to challenge the idea that this was somehow obvious.

Fwiw, I had tried to solve the OP without benefit of this theorem. Using matrices to represent the relationships between (a) the applied voltages and the input currents and (b) the applied voltages and the resulting voltages at the next column, I obtained a recurrence relation which led to a matrix equation of the form A² = B (B known). I assume it is reasonable to solve that by diagonalisation etc., but kept getting going wrong in the algebra and gave up.

 

[dauto]

The math behind the theorem can get quite complex, no doubt. By I think it is quite intuitive based on the linear vector space argument I provided.