What is the general equation for a mutating variable in a 3rd degree function?

[mireazma]

Hello.
Long time, no see. From all the forums I'm a member of, I feel this is the most strange to me as my math is very basic. So, here is what I'd be thankful to be helped with:

I'm making a "mechanic" that I'm going to use in game and software developing for tons of times if I'll pull it through (God help!). It would take months for me to solve this and I hope anyone here would be willing to help and of course would know the necessary math for it.
It's about a graph:

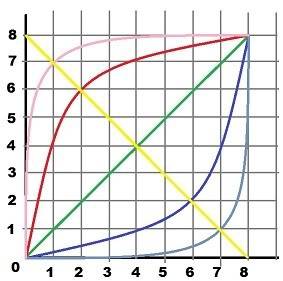
I'll do my best to explain what I want. I haven't done math since elementary so I'll use improper language and I'll let the intuition guide me; you can swear - I can't hear you

Every of the light red, red, green, blue and light blue curves has an unique function, right?
But they have something in common, in fact it's all the same except for one little variable that should... "mutate".
I want to find the magic function and the mutating variable, to work for any of the colored solutions. So it's a 2-step process:

1. Find the general multitude of functions/equations or better said -- the equation with the mutating unknown, when we know:
- start x,y (in our case 0,0)
- end x,y (in our case 8,8)
- the functions have the horizontal and vertical asymptotes (I hardly know from wikipedia what an asymptote means)

2. We further replace the mutating unknown with a numerical value and so find the final equation.
The value to replace the unknown is found like in the following example:
We want to find the magic equation for the blue solution. So, the reference yellow line must cross point(0, end y) and point(end x, 0) that's (0,8) and (8,0). On this line, from the middle of the linear green = (4,4) to the blue solution, we know D = 2* sqrt(2).
So, based on D we find the numerical value for the mutating unknown.
Now I reckon the mutating unknown raises logarithmically as D raises linearly So I'd use the yellow reference line and D instead of just the mutating unknown, so to be more intuitive/straightforward for the user/player.

So we feed in 0,0; 8,8; 2*sqrt(2) and "compose" the magic equation.
Of course, for any x we feed in the magic equation/function, we get the corresponding y of the blue solution.

If it looks too creepy at least give me a hint on step 1 and I'll die trying to solve step 2 from there.
I thank you even for only getting here with reading.

 

[micromass]

For the first problem, this should be the functions you need to use:

f(x)=\sqrt[n]{1-(-\frac{x}{8}+1)^n}

where n\in ]0,+\infty[ would be your magic parameter. The function described your curves very well, and in n=1 it gives the linear (green) curve.

I'm still trying to figure out what exactly you mean with the second part of your post, it's a bit hazy...

 

[mireazma]

Thank you very much. Man that was fast. What if I change start and end points?
I can't relate them to the function...

Now that I read your reply I realize that the 2nd part is... a separate function by itself.
f(D) = n

OFFTOPIC:
I saw your sig in another thread and couldn't ask there. So I do it here: Who said it?

 

[micromass]

Thank you very much. Man that was fast. What if I change start and end points?
I can't relate them to the function...

Hmm, that's an annoying question (nothing personal, I'm just bad at these things). Well, if you want to change the end points to (a,a), then the equation becomes

f(x)=a\sqrt[n]{1-\left(-\frac{x}{a}+1\right)^n}

(also I forgot the factor 8 in front of my first equation). If you also want to change the begin point, then it gets a bit more complicated. I'll see if I can figure it out...

Now that I read your reply I realize that the 2nd part is... a separate function by itself.
f(D) = n

Yes, and I think I understood what you wanted to do in your second point. I'll see what I can do.

OFFTOPIC:
I saw your sig in another thread and couldn't ask there. So I do it here: Who said it?

Bob Dylan

 

[micromass]

OK, your general function, with begin points (a,b) and end points (c,d) is

(d-b)\sqrt[n]{1-\left(-\frac{x-a}{c-a}+1\right)^n}+b

Now, your second question...

 

[mireazma]

Thank you so much. You already did very much, Please, don't mind the starting point. And with the second part, don't waste too much of your time. I feel in debt already
LE:
Oops! too late.

 

[mireazma]

At a second thought, the 2nd part isn't such a big issue. I could simply estimate a rough linear-logarithmic function; the user won't notice too much. The precision isn't crucial.
LE:
I know I sound fawning but I totally respect hard work and hard mind. I realize that I'm 2566 posts away from you and the same many time units necessary to compute something.