What is the Geometric Relationship Between Vectors and Their Components?

[nothing123]

The question says:

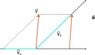
By rearranging these vectors, determine and explain the pattern formed by the heads of these vectors.

http://img131.imageshack.us/img131/5981/pattern4tp.png

 

[andrevdh]

Lets call the vector $\vec V$ and its change $\Delta \vec V$.
It is obvious that the magnitude of the change in the vector stays the same $\Delta V=const$. What about the the direction of this change in the vector? Well both $\Delta u$ and $\Delta v$ stays the same from the one vector to the other, so from the one vector to the other the change in the vector stays the same both in magnitude and direction. What curve will the heads of the vectors form according to this reasoning?

 

[siddharth]

andrevdh, I think I've missed something, but isn't the answer already drawn in the diagram?

 

[berkeman]

I would try starting with the ordering GL...AR, because that sort of looks like snapshots of a changing velocity. Not sure that the changing lengths of the vectors would correlate best to, though. Maybe it's from an elliptical orbital path? Interesting problem.

 

[siddharth]

I don't understand this question. Can anyone tell me what are the vectors which are to be rearranged?

 

[Gokul43201]

This question makes no sense to me either. But in any case, we must expect, as per the guidelines, some effort from the OP before launching into a discussion of the solution.

 

[nothing123]

the vectors are from the points on the horizontal line to the points on the sloped line. ex. AR, CP etc. you might have missed the little arrows. the pattern may have to do with the vectors u and v, for example AR = 7v - u, BQ = 6v - 2u

any ideas?

 

[andrevdh]

The diagram depicts a vector changing in magnitude and direction, starting from vector $\vec{AR}$ to $\vec{GL}$ (I guess). The change in the vector, $\Delta \vec V$, is constant in direction and magnitude. When adding this change in the vector to the "old" vector you get the "new" vector. The new vector is from the end of the old vector to the tip of the change in the vector. Since this vector change points in the same direction and is the same magnitude they will form a straight line at regular intervals for the heads of subsequent new vectors.

 

[nothing123]

andrevdh, thanks for your attempt at an explanation, you seem confident in your answer. however, i still can't grasp the bulk of what your trying to say.

the change in the vector (as it goes from AR to GL) - is it -u and +v for each succeeding vector?

"The new vector is from the end of the old vector to the tip of the change in the vector." - will you care to clairfy what your saying here?

 

[andrevdh]

The vectors are displaced relative to each other as you go from one to the next. One can see that the change in the "x-component", which I called $$\Delta u$$ and the change in the "y-component", which I called $$\Delta v$$ (according to the vectors indicated at the origin) is constant in magnitude and direction from one vector to the next. This means that the resultant vector change, which I chose to call $$\Delta \vec V$$, will be constant in both magnitude and direction.

 

[andrevdh]

The $$\vec u$$ and $$\vec v$$ components of the vector $$\vec V$$ are as indicated in the attachment. This means that the little "intervals" along these vectors between the endpoints of the vectors in the original drawing posted by nothing123 are the components of the vector difference, $$\Delta \vec V$$, for the subsequent vectors. The vector change from one to the next therefore stays constant in magnitude and direction. Which means that as one progress from the one vector to the next that these vector differences will form a straight line at regular intervals for the heads of the "new" vectors.

 

[andrevdh]

The blue vectors are the components of the old vector in the first attachment, while the green ones are the components of the new vector. The change in these components are the vectors $$\Delta u$$ and $$\Delta v$$. These two add up to produce the change in the old vector $$\Delta V$$.

The second attachment show how the change in the vector and the old vector produces the new vector.