What is the height of the cliff in this scenario?

[ramz]

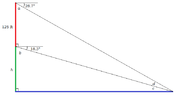
A tower 125 feet high is on a cliff on the bank of a river. From the top of the tower, the angle of depression of a point on the opposite shore is 28.7 degrees. From the base of the tower, the angle of depression of the same point is 18.3 degrees. Find the height of the cliff. (Assume the cliff is perpendicular to the river.)

Please help me to solve this problem.

 

[Prove It]

Have you at least drawn a diagram? Identified a triangle? Filled in all the information you can about that triangle?

 

[ramz]

Have you at least drawn a diagram? Identified a triangle? Filled in all the information you can about that triangle?

That's my problem too, to interpret the problem and make an illustration.

- - - Updated - - -

Please help me to interpret the problem and make an illustration or diagram because the diagram is not given. Thanks

 

[MarkFL]

Here is a diagram:

View attachment 4818

Can you begin by finding the values of the angles labeled $a,\,b,\,c,\,d$?

 

[ramz]

Thanks.

 

[ramz]

The height of the cliff is 190.71 ft., am i right?

 

[MarkFL]

Well, we know:

$$a=90^{\circ}-28.7^{\circ}=61.3^{\circ}$$

$$a=90^{\circ}-18.3^{\circ}=71.7^{\circ}$$

$$c=18.3^{\circ}$$

$$d=28.7^{\circ}-18.3^{\circ}=10.4^{\circ}$$

If we let $\ell$ be the side common to both triangles, we may use the law of sines to state:

$$\frac{\ell}{\sin\left(90^{\circ}\right)}=\frac{h}{\sin(c)}\implies h=\ell\sin(c)$$

$$\frac{\ell}{\sin(a)}=\frac{125\text{ ft}}{\sin(d)}\implies\ell=\frac{125\sin(a)}{\sin(d)}\text{ ft}$$

And so we find:

$$h=\frac{125\sin(a)\sin(c)}{\sin(d)}\text{ ft}\approx206.4\text{ ft}$$