- #1
samgrace
- 27
- 0
The energy changes correspond to infrared, h_bar * w.
Which particles are actually oscillating? The neutrons or the electrons?
Is it the electrons that fill up the stationary states, electronic configuration, or is it the nucleons that fill up the states?
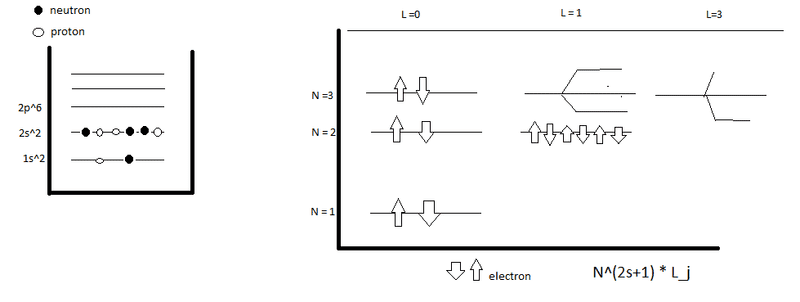
Which particles are actually oscillating? The neutrons or the electrons?
Is it the electrons that fill up the stationary states, electronic configuration, or is it the nucleons that fill up the states?