What is the induced magnetic force on this closed current loop?

[zenterix]

Homework Statement

In the figure below we have a conducting bar (green) moving through a region of uniform magnetic field $\vec{B}=-B\hat{k}$ by sliding along two frictionless conducting rails (orange) that are a distance $w$ apart and connected together by a resistor with resistance $R$.

Relevant Equations

Let an external force $\vec{F}_{ext}$ be applied so that the conductor moves to the right with constant velocity $\vec{v}=v\hat{i}$.

Below I will go through derivations I saw in some notes from MIT OCW's 8.02 "Electricity and Magnetism".

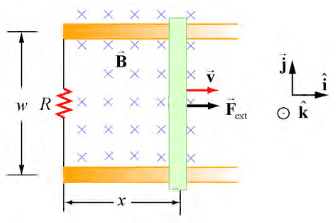
We thus have a closed loop.

Let the normal vector be $\hat{n}=\hat{k}$.

Then, the area vector is $\vec{A}=A\hat{k}$.

The magnetic flux through this loop is

$$\Phi_B=\vec{B}\cdot\vec{A}=(-B\hat{k})\cdot (A\hat{k})=-BA=-Bwx$$

and

$$\frac{d\Phi_B}{dt}=-Bwv=-\mathcal{E}$$

where $v=\frac{dx}{dt}$.

Thus,

$$\mathcal{E}=Bwv >0$$

which means that relative to our choice of normal vector, the current $I=\frac{\mathcal{E}}{R}$ flows counterclockwise.

A charge carrier with charge $q$ in the moving bar experiences a magnetic force

$$\vec{F}_B=q\vec{v}\times \vec{B}$$

$$=qv\hat{i}\times B(-\hat{k})=qvB\hat{j}$$

Then there is the following snippet

The magnetic field is not actually doing the work; the external force that is pulling the bar is doing the work. In order to see why, we first observe that the emf is causing charge carriers to move upward in the bar. The charge carrier has an additional vertical component of velocity

$$\vec{v}_{carrier}=v\hat{i}+u\hat{j}$$

Therefore the magnetic force on the charge carrier is given by

$$\vec{F}_B=q\vec{v}_{carrier}\times\vec{B}=q(v\hat{i}+u\hat{j})\times B(-\hat{k})$$

$$=qvB\hat{j}-quB\hat{i}$$

The external force must exactly oppose the $x$-component of the magnetic force in order to keep the bar moving at a constant speed.

$$\vec{F}_{ext}=quB\hat{i}$$

If a charge carrier moves from the bottom to the top of the bar in $\Delta t$ then $w=u\Delta t$.

The bar is also moving in the positive $x$-direction by an amount $\Delta x=v\Delta t=\frac{vw}{u}$.

The displacement vector is $\Delta \vec{s}=(\frac{vw}{u}\hat{i}+w\hat{j}$ and we can easily show that $\vec{F}_B\times \Delta \vec{s}=0$.

At this point, let me just recap what we have done.

1) calculated magnetic flux through the loop

2) the negative of the derivative of this magnetic flux is the emf.

3) calculated the magnetic force experienced by a charge in the conducting bar.

4) verified that this force does no work

5) equated the $x$-component of this force to the external force applied to the bar

And now we get to my question.

We have already determined that there is a counterclockwise current in the bar and rails.

Therefore there is an induced magnetic force $\vec{F}_{ind}$ experienced by current in the bar as the bar moves to the right given by

$$\vec{F}_{ind}=I(w\hat{j})\times (-B\hat{k})=-IwB\hat{i}=-\left ( \frac{B^2w^2v}{R}\right )\hat{i}$$

that is in the opposite direction of $\vec{v}$.

For the bar to move at a constant velocity, the net force acting on it must be zero. This means that the external agent must supply a force

$$\vec{F}_{ext}=-\vec{F}_{ind}=\left (\frac{B^2l^2v}{R}\right )\hat{i}$$

What the heck is this induced magnetic force?

 

[BvU]

It's called the Lorentz force

$\$

 

[kuruman]

Since there is an induced current $I_{ind.}$ through the bar and the bar is in the magnetic field ##\mathbf B it is, as @BvU explained to Lorentz force $\mathbf F=I_{ind.}~\mathbf w\times \mathbf B$. Here, $\mathbf w$ is a vector of magnitude $w$ (the length of the bar) and points in the direction of the current. Note that, since the induced current always opposes changes in the magnetic flux, it will always oppose any change in the motion that an external force (or torque) will try to introduce. Thus, it acts like a friction of sorts. The effect itself is often referred to as magnetic braking. Look it up.

 

[zenterix]

The induced magnetic force I am asking about is actually something kind of obvious that I simply missed.

The velocity of the conducting bar as a whole to the right means that a charge carrier in the bar feels a force $\vec{F}_B=qvB\hat{j}$.

From Faraday's Law, we know that this generates an emf in the loop which generates a counterclockwise current.

A charge carrier in the conducting rod now has a component of velocity in the $\hat{j}$ direction.

The induced magnetic force is the new component of magnetic force on the bar due to this new direction of velocity.

It acts in the $-\hat{i}$ direction and has the effect of decelerating the bar. We can compute the force as follows

$$\vec{F}_{ind}=\int_{bar} Id\vec{s}\times\vec{B}=I\left (\int d\vec{s}\right )\times B(-\hat{k})$$

$$=Iw\hat{j}\times B(-\hat{k})$$

$$=IwB(-\hat{i})$$

$$=\left ( \frac{Bvw}{R}\right )wB(-\hat{i})$$

$$=\frac{B^2w^2v}{R}(-\hat{i})$$

For the bar to keep moving with a constant speed, the external force must be $-\vec{F}_{ind}$.

Note the following.

The initial velocity in the $\hat{i}$ direction induced a current (via effect of magnetic force and resulting electromotive force), this current generated a magnetic field (which is an example of Lenz's law), and the presence of the current means the initial magnetic field exerts a force on the bar in the $-\hat{i}$ direction.

The power delivered by $\vec{F}_{ext}$ is

$$P=\vec{F}_{ext}\cdot\vec{v}=F_{ext}v=\left (\frac{B^2w^2 v}{R}\right ) v$$

$$=\frac{(Bwv)^2}{R}=\frac{\mathcal{E}^2}{R}=I^2R$$

which is the power dissipated in the resistor.

If at some point in time $\vec{F}_{ext}$ goes to zero then the bar decelerates due to $\vec{F}_{ind}$.

 

[BvU]

Bravo !

 

[kuruman]

If at some point in time $\vec{F}_{ext}$ goes to zero then the bar decelerates due to $\vec{F}_{ind}$.

You can push this even more if you wish. From Newton's second law, the equation of motion for the bar of mass $m$ is $$m\frac{dv}{dt}=-\frac{B^2w^2}{R}v+F_{ext}.$$Suggestion I. The bar is at rest when the external force is applied at $t=0$. Find an expression for the velocity $v(t)$ of the bar.

Suggestion II. The bar is at rest when it is given a sharp kick at $t=0$ so that it starts with initial velocity $v_0$ to the right with no external force $F_{ext}$ acting on it. Show that when the bar comes to rest the total energy dissipated in the resistor is $E_{dis.}=\frac{1}{2}mv_0^2$.

You don't have to do these, but I still remember a deep sense of satisfaction when I first did them many years ago.

 

[zenterix]

@kuruman I will do this in steps in the following posts.

As a first case, let me consider your suggestion II.

Let $\vec{F}_{ext}=\delta(t)$.

Let $k=\frac{B^2w^2}{R}$.

$$m\dot{v}+kv=\delta(t)\tag{1}$$

Let's assume rest initial conditions: $v(0)=0$ and $\dot{v}=0$.

The homogeneous solution to (1) is

$$v_h(t)=Ce^{-kt}\tag{2}$$

By using the rest initial conditions we can easily show that for $t<0$ we have $v(t)=0$.

Now consider $t>0$.

We need to solve the IVP

$$m\dot{v}+kv=0$$

$$v(0^+)=\frac{1}{m}$$

We have the same homogeneous solution (2).

But now, we have

$$v(0^+)=C=\frac{1}{m}$$

Thus, for $t>0$ we have $v(t)=\frac{1}{m}e^{-kt}$.

Putting everything together we have

$$v(t)=\begin{cases} 0,\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ t<0 \\ \frac{1}{m}e^{-\frac{B^2w^2}{mR}t},\ \ \ \ \ t>0\end{cases}$$

Let's call this the unit impulse response of the system, $w(t)$.

We see that we get a sharp kick that takes the velocity to $\frac{1}{m}$ at time $0^+$ and it decays exponentially to zero from there.

 

[kuruman]

Nice. To complete the question, you need to show that the kinetic energy of the bar is dissipated as heat in the resistor. This makes the situation analogous to giving a block resting on a table top a sharp kick on and have its kinetic energy dissipate as frictional heat.

 

[zenterix]

Next let's consider the case where $\vec{F}_{ext}=Fu(t)$ where $u(t)$ is the Heaviside unit step function.

That is, the external force is zero for $t<0$ and then is constant at $F$ for $t>0$.

Let's use rest initial conditions again, $v(0)=\dot{v}=0$.

Using Green's formula, we can find the system response to this external force.

$$v(t)=w(t)*(Fu(t))$$

$$=\int_{0^-}^{t^+} w(\tau)Fu(t-\tau)d\tau$$

$$=F\int_{0^-}^{t^+} w(\tau)d\tau$$

$$=F\int_{0^-}^{t^+} \frac{1}{m}e^{-\frac{B^2w^2}{mR}\tau}d\tau$$

$$=\left . -\frac{F}{m}\frac{mR}{B^2w^2}e^{-\frac{B^2w^2}{mR}\tau} \right |_0^t$$

$$=\frac{FR}{B^2w^2}\left (1-e^{-\frac{B^2w^2t}{mR}}\right )$$

Here we see that the velocity starts at 0 and increases to $\frac{FR}{B^2w^2}$ as $t\to\infty$.

If we choose $F=\frac{B^2w^2v}{R}=-F_{ind}$ then we get

$$v(t)=v\left (1-e^{-\frac{B^2w^2t}{mR}}\right )$$

where $v$ is a constant speed.

 

[zenterix]

If we combine the two cases then

$$F_{ext}(t)=mv\delta(t)-F_{ind}u(t)$$

which means we are giving the bar a strong initial kick to get the speed up to $v$ and then we keep the force constant at $-F_{ind}=\frac{B^2w^2v}{R}$.

The solution to the differential equation

$$m\dot{v}+kv=mv\delta(t)+\frac{B^2w^2v}{R}u(t)$$

is obtained by superposition and for $t>0$ is

$$v(t)=ve^{-\frac{B^2w^2}{mR}t}+v(1-e^{-\frac{B^2w^2}{mR}t})$$

$$=v$$

Now let me have a look at the energy considerations you brought up.

 

[zenterix]

Let's consider the case of $F_{ext}(t)=mv\delta(t)$.

That is, we give an initial impulse that takes the speed up to $v$ and then the external force is zero from then on.

Then $v(t)=ve^{-\frac{B^2w^2}{mR}t}$ for $t>0$.

Consider kinetic energy right after the initial kick

$$K(0^+)=\frac{mv^2}{2}$$

and after the conducting bar comes to rest (at $t=\infty$).

$$K(\infty)=0$$

As I calculated in posts #1 and #4 above the emf in the loop is $\mathcal{E}=Bwv(t)$ and the current is therefore

$$I=\frac{\mathcal{E}}{R}=\frac{Bwv(t)}{R}$$

The power through the resistor is

$$P(t)=\mathcal{E}I=I^2R=\frac{B^2w^2v^2(t)}{R}$$

$$=\frac{B^2w^2v^2}{R}e^{-\frac{2B^2w^2t}{mR}}$$

To obtain the total energy dissipated through the resistor we need to integrate power

$$\int_0^\infty P(t) dt$$

$$=\int_0^\infty \frac{B^2w^2v^2}{R}e^{-\frac{2B^2w^2t}{mR}} dt$$

$$=\left .-\frac{B^2w^2v^2}{R}\frac{mR}{2B^2w^2}e^{-\frac{2B^2w^2t}{mR}} \right |_0^\infty$$

$$=\frac{mv^2}{2}$$

What we see is that the magnitude of the total energy dissipated through the resistor equals the magnitude of the change in kinetic energy of the conducting bar.

Considering the signs, we have that the energy dissipated between $t=0$ and $t=\infty$ is the negative of the change in kinetic energy in this time interval.

 

[zenterix]

@kuruman Indeed very high satisfaction from this calculation.

Many doubts still about the whole ordeal. I will try to show one in my next post.

 

[kuruman]

Congratulations! You have mastered the bar-sliding-on-frictionless-rails-in-a-uniform-B-field. If you were my student, I would give you an A++, for correctness, clarity of presentation, rigor and parsimony above and beyond expectations.