What is the Largest Quantum Number for Li3+ with a 60 Å Orbital Radius?

  • #1
hassony
1
0
Threads moved from a technical forum so no Homework Template is shown.
TL;DR Summary: Quantum number of a state

What is the largest quantum number of a state of the Li3+ ion with an orbital radius equal to 60 A?

I tried solving the question as below
IMG_1470.jpeg
 
Physics news on Phys.org
  • #2
Apart from belonging in the homework section, Li3+ is a bare nucleus. It has no electrons.
 
  • #3
Apart from Li3+ being a bare nucleus, ##\sqrt{\dfrac{60\times 3}{0.529}}=18## or ##20## to one sig. fig.
 

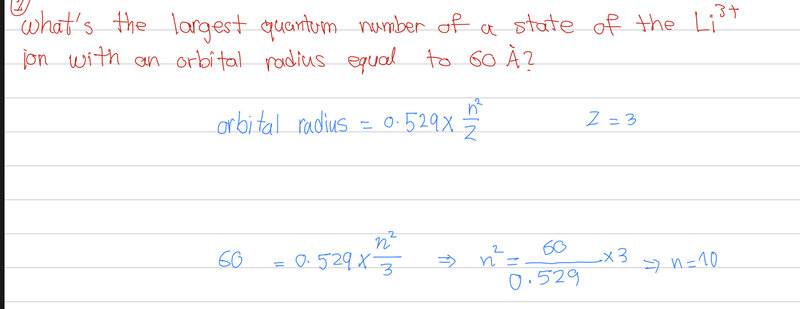
Related to What is the Largest Quantum Number for Li3+ with a 60 Å Orbital Radius?

What is the significance of the quantum number in the context of Li3+?

The quantum number in this context is significant because it helps describe the energy level and spatial distribution of the electron in the Li3+ ion. Specifically, it indicates the principal quantum number (n), which determines the size of the orbital where the electron is likely to be found.

How do you determine the principal quantum number for an electron in a given orbital radius?

The principal quantum number (n) can be determined using the Bohr model of the atom, which relates the orbital radius (r) to the quantum number. For hydrogen-like ions such as Li3+, the formula r = n^2 * a0 / Z can be used, where a0 is the Bohr radius (approximately 0.529 Å) and Z is the atomic number. Solving for n when r is given allows you to find the quantum number.

What is the Bohr radius, and why is it important in this calculation?

The Bohr radius (a0) is a physical constant that represents the most probable distance between the nucleus and the electron in a hydrogen atom in its ground state. It is important in this calculation because it provides a scale for measuring the size of electron orbits in atoms and ions. For lithium with a +3 charge (Li3+), the Bohr radius is used to determine the relationship between the orbital radius and the quantum number.

How do you apply the formula to find the largest quantum number for Li3+ with a 60 Å orbital radius?

To find the largest quantum number for Li3+ with a 60 Å orbital radius, you use the formula r = n^2 * a0 / Z. Plugging in the values, 60 Å = n^2 * 0.529 Å / 3. Solving for n, you get n = sqrt((60 * 3) / 0.529), which approximately equals 17. Thus, the largest quantum number is n = 17.

Why is it important to consider the charge of the ion (Li3+) in this calculation?

The charge of the ion (Li3+) is important because it affects the effective nuclear charge (Z) experienced by the electron. In this case, the charge is +3, meaning the electron experiences a stronger attraction to the nucleus compared to a neutral lithium atom. This changes the orbital radius for a given quantum number, making the calculation specific to the ion's charge state.

Similar threads

Find the location knowing the resonance using Kepler's third law
    • Introductory Physics Homework Help
Replies
2
Views
590
Find the unkown tensions and masses in the situation below
    • Introductory Physics Homework Help
Replies
8
Views
522
Shielding or principal quantum number predicts Covalent or Ionic?
    • Biology and Chemistry Homework Help
Replies
0
Views
264
Throwing a baseball while standing on an Asteroid
    • Introductory Physics Homework Help
Replies
5
Views
2K
Find at what rate the orbit radius will grow
    • Introductory Physics Homework Help
Replies
30
Views
766
Radius of the electron orbit in a Hydrogen atom
    • Introductory Physics Homework Help
Replies
15
Views
2K
Question about Projectile Motion: Throwing a Flower Pot from a Balcony
    • Introductory Physics Homework Help
Replies
18
Views
418
Find the possible outcomes of ]##L^2## and ##L_{z}##
    • Advanced Physics Homework Help
Replies
21
Views
408
Basics of forces/torques and fulcrum
    • Introductory Physics Homework Help
Replies
6
Views
932
Errors in Experiment with Low and High Conductivity Materials
    • Introductory Physics Homework Help
Replies
2
Views
546

Hot Threads

Recent Insights

Back
Top