- #1
Norpyx
- 5
- 0
Overview
I've been struggling at this problem for about 3 days now. I've posted it on a couple forums will no answers, so maybe I'll get a solution here. Thanks in advance!
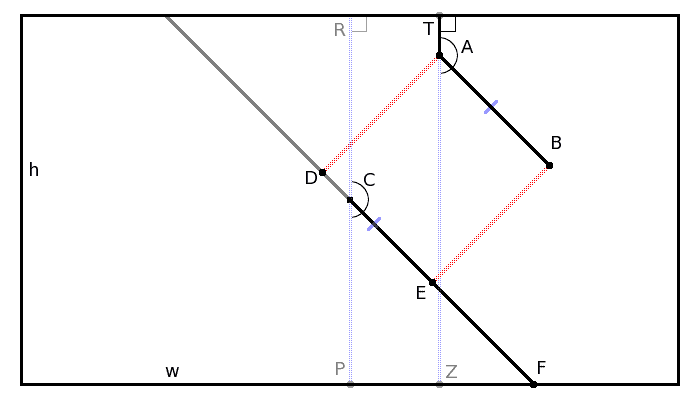
Plain Diagram: http://www.swivelgames.com/projects/ideas/circlepoints/getseglength_simpler.png
Known: A, B, C, P, R, T, Z, h, w
Need: D, E, F; Length of dcef and ef segments
Y axis is inverted!
(0,0) is at top left corner of rectangle
Known Data
h = 600
w = 800
C is at (w/2,h2) = (400,300)
R is at (400,0)
P is at (400,600)
A is at (534,88)
B is at (740,296)
T is at (534,0)
Z is at (534,600)
∠TAB = 135°
∠ZAB = 45°
∠RCE = ∠TAB
∠PCE = ∠ZAB
Problem Solving
∠ZFE = 90 - ∠PCE
∠ZFE = 45°
segCP = segRC = 400
segCF = sin(∠PCF) × segCP
segCF = sin(45) × 400
segCF = 282.8427125
The Question!
Now all I really need is the length of segEF to solve the problem, since we know that segDE = segAB.
So segDF = segDE + segEF
Can anyone help me get segEF?
Something to note: This is a real-world problem where ∠TAB will be anywhere from 0° to 360°, which in-turn would affect what side and position F would be. And ∠RCF always = ∠TAB
I've been struggling at this problem for about 3 days now. I've posted it on a couple forums will no answers, so maybe I'll get a solution here. Thanks in advance!
Plain Diagram: http://www.swivelgames.com/projects/ideas/circlepoints/getseglength_simpler.png
Known: A, B, C, P, R, T, Z, h, w
Need: D, E, F; Length of dcef and ef segments
Y axis is inverted!
(0,0) is at top left corner of rectangle
Known Data
h = 600
w = 800
C is at (w/2,h2) = (400,300)
R is at (400,0)
P is at (400,600)
A is at (534,88)
B is at (740,296)
T is at (534,0)
Z is at (534,600)
∠TAB = 135°
∠ZAB = 45°
∠RCE = ∠TAB
∠PCE = ∠ZAB
Problem Solving
∠ZFE = 90 - ∠PCE
∠ZFE = 45°
segCP = segRC = 400
segCF = sin(∠PCF) × segCP
segCF = sin(45) × 400
segCF = 282.8427125
The Question!
Now all I really need is the length of segEF to solve the problem, since we know that segDE = segAB.
So segDF = segDE + segEF
Can anyone help me get segEF?
Something to note: This is a real-world problem where ∠TAB will be anywhere from 0° to 360°, which in-turn would affect what side and position F would be. And ∠RCF always = ∠TAB