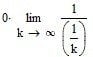What is the limit of k over k squared?

[icystrike]

Homework Statement

[PLAIN]http://img190.imageshack.us/img190/3204/84956253.jpg

This is not a homework.. I am wondering if it should really be zero or indeterminant form and i need a explanation(dont hesitate to quote from theorems)

Homework Equations

The Attempt at a Solution

 

[HallsofIvy]

The first two, $\lim_{k\to\infty} 0= 0$ and $\lim_{k\to\infty} 0\cdot k= 0$ are correct- they are both the limit of the sequence 0, 0, 0, ...

The third one is not "inderminant"- it does not exist because $\lim_{k\to\infty} k$ does not exist.

 

[icystrike]

Do pardon me.. why $\lim_{k\to\infty} k$ does not exist?

(I'm suspecting the determinant form of the indeterminant is 0)

 

[Mark44]

$$\lim_{k \to \infty} k = \infty$$

The limit doesn't actually exist, since $\infty$ isn't a finite number. All this says is that as k gets large without bound, then (obviously) k gets large without bound. This is not one of the indeterminate forms (no such word as indeterminant) such as the following:
$$\left[\frac{\infty}{\infty}\right] \left[\infty - \infty\right]\\ \left[\frac{0}{0}\right]\\ \left[1^{\infty}\right]$$

 

[icystrike]

$$\lim_{k \to \infty} k = \infty$$

The limit doesn't actually exist, since $\infty$ isn't a finite number. All this says is that as k gets large without bound, then (obviously) k gets large without bound. This is not one of the indeterminate forms (no such word as indeterminant) such as the following:
$$\left[\frac{\infty}{\infty}\right] \left[\infty - \infty\right]\\ \left[\frac{0}{0}\right]\\ \left[1^{\infty}\right]$$

However, we can always change into

which is indeed 0/0

 

[micromass]

The rule

$$\lim_{n\rightarrow +\infty}{x_ny_n}=\lim_{n\rightarrow +\infty}{x_n}\lim_{n\rightarrow +\infty}{y_n}$$

which you use, does not always hold. It only holds if the two limits on the right-hand side exists. And this is not the case here...

 

[Mark44]

However, we can always change into

which is indeed 0/0

Indeed it is not. The denominator is approaching 0, but the numerator is 1.

 

[icystrike]

There is a 0 outside the limit won't it make it 0/0?
Secondly, if limit of k as k tends to infinity does not exist, how about limit of k/k^2 as k tends to inifinity? ( since you can break up the limit to (lim k)/(lim k^2)

 

[Mark44]

That font is so small in that thumbnail that I took it to be 0 - the rest.

In any case, I don't see the point in going to complicated expressions just to represent
$$\lim_{k \to \infty} k = \infty$$.

In one sense, which is what HallsOfIvy was saying, the limit doesn't exist, since infinity isn't a value in the real number system. To say that the limit is infinity just means that the value of k gets larger and larger as k gets larger and larger.

$$\lim_{k \to \infty} \frac{k}{k^2} = \lim_{k \to \infty} \frac{1}{k} = 0$$

The first expression is one of the indeterminate forms I mentioned earlier in this thread. It can be simplified to the second expression above, which has a limit of 0.