What is the Magnitude of Acceleration for Point B in a Moving Piston System?

[Clancy]

Homework Statement

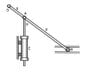
The piston is moving up at constant velocity 2.2m/s, the distance p is 1m, the distance q is 0.1m, the angle ɵ is 52 degrees.
Find the magnitude of the acceleration of B

Homework Equations

Vb = Va + Vb/a
Ab = Aa + Ab/a

The Attempt at a Solution

In general terms I found Vb/a to be (V/sin(ɵ))
The normal component of the acceleration of Ab/a is then [(V/sin(ɵ))^2]/p
I then got a general solution of Ab = ([(V/sin(ɵ))^2]/p)/sin(ɵ)

I don't think this is right however as this is an online homework, my solution gives the acceleration of B as 9.9 m/ss where the online answer is rounded to 13m/ss.

Any help with this would be great, the actual answer won't be 13 as the lecturer rounded it a lot I think. If anyone could just try this and see if they get close to 13 I'd very much appreciate it.

 

[tiny-tim]

Hi Clancy!

In general terms I found Vb/a to be (V/sin(ɵ))
The normal component of the acceleration of Ab/a is then [(V/sin(ɵ))^2]/p
I then got a general solution of Ab = ([(V/sin(ɵ))^2]/p)/sin(ɵ)

Sorry, I don't understand this.

Start by finding the lengths CA and CB in terms of p and θ.