- #1
QuarkCharmer
- 1,051
- 3
Gravitation Force (Solved, thanks)
A sphere with mass of 65kg and center at origin. Another sphere with mass 79kg at point (0,3), also centered at origin.
A.) What is the magnitude of the net gravitational force due to these objects on a third uniform sphere with mass 0.490 kg placed at the point (4,0)
[tex]F_{g} = \frac{GMm}{r^{2}}[/tex]
[tex]G = 6.67(10^{-11})[/tex]
I made this image to help:
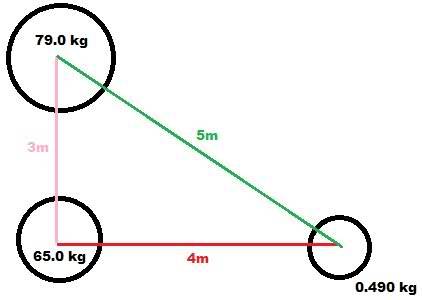
Force from the 79kg sphere:
[tex]FG_{1}=\frac{G(.490)(79)}{5^{2}}[/tex]
Force from the 65kg sphere
[tex]FG_{2}=\frac{G(.490)(65)}{4^{2}}[/tex]
So the net force on the .490 kg sphere is given by:
[tex]\sqrt{(FG_{2} + FG_{1}cos(tan^{-1}(\frac{3}{4})))^{2}+(FG_{1}sin(tan^{-1}(\frac{3}{4})))^{2}}[/tex]
I get the net force on the 0.490 kg sphere to be 3.48 N. Which is incorrect? I don't know what is wrong.
Homework Statement
A sphere with mass of 65kg and center at origin. Another sphere with mass 79kg at point (0,3), also centered at origin.
A.) What is the magnitude of the net gravitational force due to these objects on a third uniform sphere with mass 0.490 kg placed at the point (4,0)
Homework Equations
[tex]F_{g} = \frac{GMm}{r^{2}}[/tex]
[tex]G = 6.67(10^{-11})[/tex]
The Attempt at a Solution
I made this image to help:
Force from the 79kg sphere:
[tex]FG_{1}=\frac{G(.490)(79)}{5^{2}}[/tex]
Force from the 65kg sphere
[tex]FG_{2}=\frac{G(.490)(65)}{4^{2}}[/tex]
So the net force on the .490 kg sphere is given by:
[tex]\sqrt{(FG_{2} + FG_{1}cos(tan^{-1}(\frac{3}{4})))^{2}+(FG_{1}sin(tan^{-1}(\frac{3}{4})))^{2}}[/tex]
I get the net force on the 0.490 kg sphere to be 3.48 N. Which is incorrect? I don't know what is wrong.
Last edited: