What Is the Maximum Acceleration of a Crate Up an Incline Before Tipping Over?

[Vladimir_Kitanov]

Homework Statement

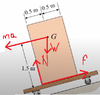
Picture

Relevant Equations

Nothing special

Correct answer is (b) 0,620 ms2

My attempt:
FBD

Equation 1. ∑Fx=0=−ma−Wsin⁡(15)+f
N=Wcos⁡15
f=Nμs=379,03N

Equation 1. ma=f−Wsin⁡15
15a=379,03−203,1
a=2,20ms2

Equation 2. ∑MG=0=−Nx+f1,5
x=0,75m

 

[Lnewqban]

What is the condition for tipping over to occur?

 

[Vladimir_Kitanov]

What is the condition for tipping over to occur?

x need to be more then 0,5

 

[Lnewqban]

And what is x?

 

[malawi_glenn]

Why did you draw the point of action for the normal force they way you did?

 

[kuruman]

For the crate to tip, a non-zero net torque is needed. I don't see a torque equation. Your value for the acceleration of 2.20 m/s² is the value at which the crate will start sliding assuming that it does not tip. If the crate tips before it starts sliding, the 2.20 m/s² cannot be the answer. You need to find another value for the acceleration at which the crate will tip assuming that it does not slip and pick the smaller of the two values as the answer. As @Lnewqban asked,

What is the condition for tipping over to occur?

That's a key issue to address.

On edit:
Your answer

x need to be more then 0,5

is a non-answer because x cannot be greater than 0.5 m.

 

[Vladimir_Kitanov]

I don't seem to understand well slipping and tipping.
I will learn more about that and then i will be back here.
:)

 

[Lnewqban]

I don't seem to understand well slipping and tipping.
I will learn more about that and then i will be back here.
:)

In order for the block to tip over, two things need to happen: a moment about the edge, and enough static friction, so the block does not slide rather than tip over.
Determining both things is the core of this problem.
You now that friction depends on normal force and coefficient of friction.
You also know that any force that has a lever or distance respect to the pivoting edge, induces a moment.

 

[Vladimir_Kitanov]

Ok i did it.
To solve this we need to find acceleration when slipping will occur and acceleration when tipping occur.
And choose smaller so it will not tip or slip.

 

[kuruman]

Ok i did it.
To solve this we need to find acceleration when slipping will occur and acceleration when tipping occur.
And choose smaller so it will not tip or slip.

Yes, that's what I suggested. Please post your work for finding the maximum acceleration before tipping occurs.

 

[Vladimir_Kitanov]

Yes, that's what I suggested. Please post your work for finding the maximum acceleration before tipping occurs.

W - weight = $W = m*9,81 = 784,8$
N - normal force On left edge because it will tip over that edge and all weight will be there.
$N = W\cos15 = 758,1$
f - friction

Equation 1$\sum F_x = 0 = ma - f + W\sin15$
$\sum M_G = 0 = -N0,5 + f1,5$ --> $f = 252,69$

From equation 1 we now find a.
$a = 0,62$

 

[kuruman]

Why will the block tip if there is no unbalanced torque acting on it? Do you understand torques? What do they do?

 

[Vladimir_Kitanov]

Why will the block tip if there is no unbalanced torque acting on it? Do you understand torques? What do they do?

Sum of all torques is 0. And it will not tip.
When we set normal force to be on edge we find maximum acceleration at at witch crate will not tip.
If acceleration is bigger then 0,62 it will tip.

 

[haruspex]

View attachment 305589

W - weight = $W = m*9,81 = 784,8$
N - normal force On left edge because it will tip over that edge and all weight will be there.
$N = W\cos15 = 758,1$
f - friction

Equation 1$\sum F_x = 0 = ma - f + W\sin15$
$\sum M_G = 0 = -N0,5 + f1,5$ --> $f = 252,69$

From equation 1 we now find a.
$a = 0,62$

You still seem to be tangling up the two cases.

In post #1, you successfully found the max acceleration assuming that it will slip rather than tip.
But then you wrote

Equation 2. ∑MG=0=−Nx+f1,5

where I assume you used the f calculated from the first case, but you should now be assuming that it will tip rather than slip, so that f value is irrelevant. Take moments about the tipping point instead.

In post #11, you made the converse error: found f assuming tip but applied that value to the slip case.

 

[Vladimir_Kitanov]

In post #11, you made the converse error: found f assuming tip but applied that value to the slip case.

That all is just tip case.I did not post solution for slip case.
For slip case i get different value for friction.

 

[haruspex]

That all is just tip case.I did not post solution for slip case.
For slip case i get different value for friction.

Sorry, you are right. I agree with your answer.