MHB What is the maximum area of the circular sector with a perimeter of 12 cm?

[mathdad]

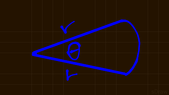
The given picture shows a circular sector with radius r cm and central angle θ (radian measure). The perimeter of the sector is 12 cm.

1. Express the area A of the sector as a function of θ. Is this a quadratic function?

2. Express the area A of the sector as a function of r. Is this a quadratic function?

3. For which value of r is the area A a maximum? What is the corressponding value of θ in this case?

Part 1

I know the area of the sector formula is A = (1/2) r^2 θ.

I simply thought the answer must be A(θ) = (1/2) r^2 θ but then I said no because the radius square should not be as part of the answer. The question is asking to express the area A of the sector as a function of theta not a function of r and θ.

The book's answer is A(θ) = (72 θ)/(2 + θ)^2. Of course, this is not a quadratic function. Where did this fraction come from? Where did 72 and 6 come from?

Part 2

Again, I quickly jumped to conclusion since I know the area of a sector formula to be A = (1/2) r^2 θ.

I said, ok, the answer must be A(r) = (1/2) r^2 θ. There it is. It is written in terms of r. I am wrong, of course. You see, θ should not be part of the answer if we must express the area A as a function of r not a function of r and θ.

The book's answer is A(r) = 6r - r^2. I recognize this to be a quadratic function. Where did 6 come from?

Part 3

I need the steps for Part 3 that will guide me to the answer. Can someone provide me with the steps?

View attachment 7911

 

[MarkFL]

We know the perimeter $P$ is:

$$P=2r+r\theta=(2+\theta)r\tag{1}$$

The area is:

$$A=\frac{1}{2}r^2\theta\tag{2}$$

(1) gives is a way to relate $r$ and $\theta$. So:

1.) solve (1) for $r$, and substitute for $r$ into (2) to get $A(\theta)$. Now, you will also have the parameter $P$ present, but it has been given, so you can just plug that in once you get the formula. What do you get?

2.) solve (1) for $\theta$, and substitute for $\theta$ into (2) to get $A(r)$. Now, as before, you will also have the parameter $P$ present, but it has been given, so you can just plug that in once you get the formula. What do you get?

 

[mathdad]

You say solve 1 for r and plug for r into 2.
Then you said to solve 1 for theta and plug for theta into 2.

Do you mean that 1 here represents the perimeter of the sector formula and 2 the area of the sector formula?

If so, I will try later tonight after work.