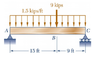
What is the maximum normal stress in a W18x46 beam?

[SteelDirigibl]

Homework Statement

Homework Equations

σ=P/A

σ=My/I

τ=VQ/It

The Attempt at a Solution

I'm on part C, pretty sure I have A and B, so I'm using a W18x46 Beam. I have drawn shear and moment diagrams. I just want to be clear on what part C is asking...
I'm assuming this point is at the end of the web, wither top of bottom, just not part of the flange. So if that's correct... it is wanting the max normal stress. Is this ging to be where moment is at it's maximum? I have determined this to be at 14.25 ft (using A as the origin), with the moment being 152.3 kip*ft.

V is at a max at C, this seems it might make more sense. but P/A just gets me 1.75 and that's the same as τ that I already found.

Reaction force at A is 21.375 kip and at C is 23.625.

Am I on the right track? Can I use the equations above, find principle stresses, and make a mohr's circle? because at this point, I have V=0, does that seem right?

I'm also not sure which I to use... the x-x axis or y-y? the I for these beams in the apendix shows x-x being 712 in⁴ and 22.5 in⁴ going by the y-y axis

Any more of my previous calculations that might be neccessary, let me know, I'll post them...

 

[SteelDirigibl]

I think I may have figured it out. I just used Mc/I where c is the distance from the neutral axis.

Beam is 18.06 in deep, minus 0.625in per each flange, is 16.85, divided by two is 8.425. I used that as C, and 712 for I. Its about 22 ksi. seems reasonable to me.