What Is the Optimal Angle Theta to Minimize Journey Time in Calculus?

[Guineafowl]

Summary: Trying to differentiate with respect to $\theta$ is entangling me in cos and sec terms.

A simple problem I found, while looking for calculus practice. Roads between home and main road are 30 mph, main road is 60mph:

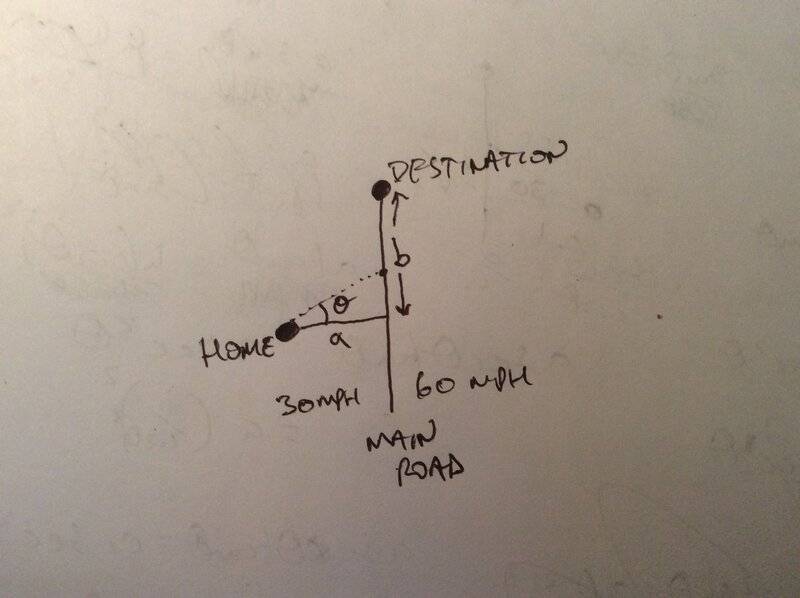
What is the optimum $\theta$ to minimise journey time?

$t = \frac {distance} {speed}$, so is a combination of the hypotenuse, and the fixed distance b minus the opposite side of the triangle formed.

In terms of $\theta$:
$t = \frac a {30\cos\theta} + \frac {b-atan\theta} {60}$

$\frac {dt} {d\theta} = \frac 1 {30} asec\theta tan\theta - \frac 1 {60}{asec^2\theta}$

Set $\frac {dt} {d\theta}$ to zero:
$$ \frac 1 {30} asec\theta tan\theta = \frac 1 {60} asec^2\theta $$
Multiply both sides by 60:
$$ 2asec\theta tan\theta = asec^2\theta $$
Divide by a:
$$ 2sec\theta tan\theta = sec^2\theta $$
Divide by $sec\theta$:
$$ 2tan\theta = sec\theta $$
Alternatively:
$$ \frac {2sin\theta} {cos\theta} = \frac 1 {cos\theta} $$
Multiply by $cos\theta$:
$$ 2sin\theta = 1 $$
$$ sin\theta = \frac 1 2 $$
$$ \theta = sin^{-1} \frac 1 2 $$
$$ \theta = 30\deg $$

And, although I’ve been puzzling over this for over an hour, in setting out the question here, I’ve got an answer. Is it correct?

 

[PhDeezNutz]

I’m sorry, I don’t understand the question. Are you allowed to travel diagonally (that is to say not on the roads)?

Are you saying we can travel diagonally with a horizontal component no greater than 30 mph and a vertical component no greater than 60 mph?

 

[Guineafowl]

The original question, from Gilbert Strang’s lecture series on the basics of calculus, imagined a network of 30mph roads between home and the main road.

I think the idea was to work out the optimum angle to aim for. This on the understanding that in the real world, you’d have to plan a ‘best fit’ route with the available roads.

In his lecture, he calculated minimum $t$ with respect to a joining point $x$, such that the diagonal journey would be $\sqrt{a^2 + x^2}$, and the remainder of the journey simply $b-x$.

He then suggests trying the same scenario with respect to $\theta$

 

[PhDeezNutz]

I got the same thing. I did things a little bit different at the end when solving for $\theta$.

$\sec \theta = 2 \tan \theta$

$\sec^2 \theta = 4 \tan^2 \theta$

$\sec^2 \theta - \tan^2 \theta = 3 \tan^2 \theta = 1$

$3 \tan^2 \theta = 1$

$\tan \theta = \frac{1}{\sqrt{3}}$

$\theta = \frac{\pi}{6}$I like your way better. At first I was trying to set up the problem in all sorts of weird ways involving Lagrange Multipliers and whatnot...turns out that was a bad idea.

 

[epenguin]

Lagrange is not exactly weird, and is highly relevant.
This is the classic least time problem, important in the history of science.
Started by Fermat and I don't remember who else, the way light travels.
Starting point of calculus of variations, in all the textbooks.
But you can do this one with elementary calculus.

 

[Guineafowl]

I got the same thing. I did things a little bit different at the end when solving for $\theta$.

$\sec \theta = 2 \tan \theta$

$\sec^2 \theta = 4 \tan^2 \theta$

$\sec^2 \theta - \tan^2 \theta = 3 \tan^2 \theta = 1$

$3 \tan^2 \theta = 1$

$\tan \theta = \frac{1}{\sqrt{3}}$

$\theta = \frac{\pi}{6}$I like your way better. At first I was trying to set up the problem in all sorts of weird ways involving Lagrange Multipliers and whatnot...turns out that was a bad idea.

Thanks for confirming that.

With your method, I’m not sure how this bit =1:
$\sec^2 \theta - \tan^2 \theta = 3 \tan^2 \theta = 1$

Another thing troubling me is how the fixed distances $a$ and $b$ disappear from the answer, since there will be values of both where 30° will miss the destination completely (small $b$ and large $a$).

 

[Steve4Physics]

Can I chip in?

In the initial equation
$t = \frac a {30\cos\theta} + \frac {b-atan\theta} {60}$
there is an in-built assumption: the last term requires that $b≥atan\theta$ in order for the term to be non-negative. This requires $tan\theta ≤\frac b a$ (taking a and b as positive values).

So, in this particular problem, the solution ($\theta = 30^o$) is only valid when $\frac b a ≥tan(30^o)$.
__________

To get $\sec^2 \theta - \tan^2 \theta = 3 \tan^2 \theta = 1$ @PhDeezNutz has used the identity $sec^2 \theta - tan^2 \theta = 1$.
___________

On a general point, I recommend combining simple algebra steps where appropriate. So for:
$\frac 1 {30} asec\theta tan\theta = \frac 1 {60} asec^2\theta$
you can quite easily:
- multiply both sides by 60;
- cancel 'a’s on both side;
- cancel 'sec's on both sides
in a single step, going straight to:
$2tan\theta = sec\theta$

 

[Guineafowl]

Thanks.

I separated out each step in the hope that you would spot where I was going wrong, but in doing so, managed to find the answer.

The late Jim Hardy, of the EE part of this forum, always used to say, ‘a question well stated is half answered’. He was certainly right in this case.

 

[PhDeezNutz]

‘a question well stated is half answered’. He was certainly right in this case.

I’ve never seen this before. But it’s profound.

 

[epenguin]

Have you noticed that your θ is independent of $a$ and $b$?

Is it obvious to you that it must be?

And what actually happens when b is small enough that your θ direction from starting point would take you beyond given arrival poin?

 

[Guineafowl]

Yes, as I say above, it’s interesting that the $a$ and $b$ terms disappear from the minimum time calculation. @Steve4Physics provided a nice explanation.The term for the vertical journey, assuming you can only travel upwards on the main road, is:
$$t = \frac {b-atan\theta} {60}$$

If $b$ is smaller than $atan\theta$, ie you join the main road after the destination, the journey time sign becomes negative, ie backwards time travel.

Also, the derivative:
$$\frac{dt}{d\theta} = \frac{1}{30}asec\theta tan\theta - \frac{1}{60}asec^2\theta$$

Has only one solution for zero, which is a minimum, and so no maxima either side.

Increasing $\theta$
For all values of $b$ (vertical distance to destination) that are less than $atan\theta$ (joining point), time travel is required.

Decreasing $\theta$
As $\theta$ reduces through 0° and towards -90°:
$cos\theta$ tends to zero and so the diagonal journey $\frac {a}{30cos\theta}$ tends to $\infty$.

$tan\theta$ tends to $\infty$ and so does the vertical journey $\frac {b-atan\theta}{60}$

 

[PeroK]

More generally, if you can travel at speed $u$ horizontally and $v > u$ vertically, then the optimum angle is $\theta = \sin^{-1}(\frac u v)$. Assuming, as above, that $b > a\tan \theta$.

 

[epenguin]

Yes, as I say above, it’s interesting that the $a$ and $b$ terms disappear from the minimum time calculation. @Steve4Physics provided a nice explanation.

By 'intuitive' I was thinking rather than anything like that, that (if given that you can cut across from $A$ at some angle θ an at 30 mph and then travel Northwards at 60 mph to $B$) if θ is angle that makes this fastest, then if $B'$ is another point further north, you get to it driving a bit further at your already maximum velocity of 60. There couldn't be a faster way to $B'$ unless there were a faster way to $B$ than the one you have already proved fastest. so the optimum θ does not depend on $B$.

Then there is my other question and perhaps other intuitive points.

"When you have solved the problem the job is not finished"

 

[Guineafowl]

By 'intuitive' I was thinking rather than anything like that, that (if given that you can cut across from $A$ at some angle θ an at 30 mph and then travel Northwards at 60 mph to $B$) if θ is angle that makes this fastest, then if $B'$ is another point further north, you get to it driving a bit further at your already maximum velocity of 60. There couldn't be a faster way to $B'$ unless there were a faster way to $B$ than the one you have already proved fastest. so the optimum θ does not depend on $B$.

Then there is my other question and perhaps other intuitive points.

"When you have solved the problem the job is not finished"

My ramblings in post #11 were an attempt to answer your questions, but I’ll try another tack.

I think the most important condition is that $b>atan\theta$

- If this is the case, then the calculations give a fastest time to join the fast road, and once you’re on there, it doesn’t matter how far along it $b$ is.

- If not the case, you’ll join after the destination and go on for ever.

For distance $a$, as it increases, with fixed $b$, the range of angles which satisfy $b>atan\theta$ becomes very small, rendering the whole calculation moot.

As $a$ decreases, the range of angles is large and allows the ratio of speeds, as pointed out by @PeroK, not $a$, to be the determining factor for optimum $\theta$.

In a nutshell, once you have established that $b>atan\theta$, you can discard both variables and the calculation reduces to $sin^{-1}(\frac u v)$.

 

[epenguin]

I think you're saying more or less the same as I was getting at.
The question of whether with your angle θ you overshoot has also come up several times, with the inequalities etc.
I think you can fast and intuitively deal with all that just turning the question around ;)

 

[PeroK]

My explanation is that as $\theta$ increases from $0$, the time must initially reduce (which can be deduced from basic trigonometry). There must then be a single minimum as $\theta$ increases. That's independent of $a$, because it's the same physical problem for any $a$.

That's why, subject to $b$ being large enough, the answer is independent of $b$ as well.

 

[Guineafowl]

Another problem, this time with integration. As you can see, this is example 12 in a textbook of electronics engineering, and I have, so far, been following the calculations using the brief guide to calculus in one of the appendices.

I can’t work out why $L$ disappears in the second step, and where the $m$ and $b$ terms have come from.

I wonder if someone long-suffering like @PeroK could take me through it, or at least point out which integration technique is being used so I can look it up.

 

[PeroK]

Another problem, this time with integration. As you can see, this is example 12 in a textbook of electronics engineering, and I have, so far, been following the calculations using the brief guide to calculus in one of the appendices.

View attachment 303271

I can’t work out why $L$ disappears in the second step, and where the $m$ and $b$ terms have come from.

I wonder if someone long-suffering like @PeroK could take me through it, or at least point out which integration technique is being used so I can look it up.

$L = 1 \ H$. And $m,b$ are general coefficients for a linear relationship, which get plugged into the next step.

 

[Steve4Physics]

Another problem, this time with integration. As you can see, this is example 12 in a textbook of electronics engineering, and I have, so far, been following the calculations using the brief guide to calculus in one of the appendices.

View attachment 303271

I can’t work out why $L$ disappears in the second step, and where the $m$ and $b$ terms have come from.

I wonder if someone long-suffering like @PeroK could take me through it, or at least point out which integration technique is being used so I can look it up.

I might be able to save @PeroK the trouble. (I am also long-suffering - though not from PF.)

The question says L = 1H. Maybe the author has made the numerical substitution - so ‘L’ apparently 'disappears'. It would have been better practice to leave the 'L' until the final expression is evaluated.

Edit. Aha. @PeroK is much faster (and no doubt longer-suffering) than me.

 

[Guineafowl]

$L=1$ is obvious. Silly of me.

$m=500$ and $b=5$; if they’re general coefficients, where did the values come from?

 

[PeroK]

$m=500$ and $b=5$; if they’re general coefficients, where did the values come from?

the problem statement specifies the linear increase in voltage.

 

[Guineafowl]

$m=\frac{5V}{0.01S}=500$?
$b=5V$ total change?

Thank you again. It might as well be magic, to me, but I’ll keep plugging away.

 

[PeroK]

$m=\frac{5V}{0.01S}=500$?
$b=5V$ total change?

Thank you again. It might as well be magic, to me, but I’ll keep plugging away.

No. We have a linear relationship $V(t) = mt +b$. If we set $t =0$, then we see that $b = V(0)$ is the initial voltage. And $m = \frac{\Delta V}{\Delta t}$.

Don't forget the units when you plug in the numbers.

 

[Guineafowl]

This is $y=mx+c$? I do remember that!

In this case, $Vapplied=500t+5$

At 12 yrs old we had an awful teacher who explained this badly, and none of us really got it.
Next year, new teacher proposed to go over it. We all groaned. He was surprised, and revealed it to be quite simple. We were surprised.

 

[PeroK]

$a,b,c,d$ whatever!

 

[Guineafowl]

$a,b,c,d$ whatever!

I suppose the next question is, can you recommend a calculus textbook that would take me from (I see you’re from the UK) GCSE maths to somewhere near grasping these calculations?

 

[PeroK]

I suppose the next question is, can you recommend a calculus textbook that would take me from (I see you’re from the UK) GCSE maths to somewhere near grasping these calculations?

I don't have a calculus textbook. There are some recommendations elsewhere on the site I think.

 

[Guineafowl]

I wonder if anyone can help me follow this:

Kirchhoff’s law tells us that, around the circuit pictured, the jump in voltage across $Vs$ equals the drop $IR + L\frac{dI}{dt}$.

They have rewritten the equation below that, and I’ve attempted follow their solution, having looked up how to do it.

To reiterate, I’m trying to solve this for $I$:

$\frac{dI}{dt} + \frac{R}{L}I = \frac{V}{L}$

substituting $I=uv$ and $\frac{dI}{dt} = u\frac{dv}{dt} + v\frac{du}{dt}$ I get:

1) $u\frac{dv}{dt} + v(\frac{du}{dt} + \frac{Ru}{L}) = \frac{V}{L}$

Setting the $v$ term to zero:

$\frac{du}{dt} = -\frac{Ru}{L}$

And solving for $u$ by substitution of variables:

$u = ke^{-\frac{Rt}{L}}$

Substituting $u$ into equation 1:

$ke^{-\frac{Rt}{L}}\frac{dv}{dt} = \frac{V}{L}$

Leaves $dv$ to calculate:

$\int dv = \frac{V}{kL} \int e^{\frac{Rt}{L}} dt$

$v=\frac{V}{kR} e^{\frac{Rt}{L}}$

Now, substituting $I=uv$:

$I = uv = \frac{V}{R} e^{-\frac{Rt}{L}}e^{\frac{Rt}{L}}$

Which doesn’t work, of course.

The answer is meant to be:

$I = \frac{V}{R} (1-e^{\frac{-t}{L/R}})$

I looked up solving homogeneous linear first-order equations, and this one is non-homogeneous. Is that something to do with it? Or the mention of the current starting at zero?

Many thanks

 

[SammyS]

I wonder if anyone can help me follow this:
View attachment 314289

Kirchhoff’s law tells us that, around the circuit pictured, the jump in voltage across $Vs$ equals the drop $IR + L\frac{dI}{dt}$.

They have rewritten the equation below that, and I’ve attempted follow their solution, having looked up how to do it.

To reiterate, I’m trying to solve this for $I$:

$\frac{dI}{dt} + \frac{R}{L}I = \frac{V}{L}$

substituting $I=uv$ and $\frac{dI}{dt} = u\frac{dv}{dt} + v\frac{du}{dt}$ I get:

1) $u\frac{dv}{dt} + v(\frac{du}{dt} + \frac{Ru}{L}) = \frac{V}{L}$

Setting the $v$ term to zero:

$\frac{du}{dt} = -\frac{Ru}{L}$

And solving for $u$ by substitution of variables:

$u = ke^{-\frac{Rt}{L}}$

Substituting $u$ into equation 1:

$ke^{-\frac{Rt}{L}}\frac{dv}{dt} = \frac{V}{L}$

Leaves $dv$ to calculate:

$\int dv = \frac{V}{kL} \int e^{\frac{Rt}{L}} dt$

$v=\frac{V}{kR} e^{\frac{Rt}{L}}$

Now, substituting $I=uv$:

$I = uv = \frac{V}{R} e^{-\frac{Rt}{L}}e^{\frac{Rt}{L}}$

Which doesn’t work, of course.

The answer is meant to be:

$I = \frac{V}{R} (1-e^{\frac{-t}{L/R}})$

I looked up solving homogeneous linear first-order equations, and this one is non-homogeneous. Is that something to do with it? Or the mention of the current starting at zero?

Many thanks

It seems to me that you should start a new thread to post this.