What is the Optimal Distance for a Frictionless Track to Minimize Time?

[NAkid]

Homework Statement

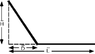
A frictionless track is to be built as shown, with L=4.60m and H=4.80m. In order to get the cart to slide from the top to the end of the track in the minimum time, how long should the distance D be? Assume that the speed of the cart on the horizontal surface is the same as at the bottom of the ramp.

Homework Equations

The Attempt at a Solution

No friction means energy is conserved.
Average velocity is distance divided by time.

using conservation laws, i get the following equation
.5mv1^2 + mgy1 = .5mv2^2 + mgy2

i set up my coordinates so that y1 is the top of the ramp, and y2 is the end, so y2=0 and we're left with .5mv1^2 + mgy1 = .5mv2^2.

the problem wants the D to minimize time, so somehow i need to express the above equation in terms of time, take a derivative, and solve setting=0.

i know v(av)=d/t, so can i substitute that expression into .5mv1^2 + mgy1 = .5mv2^2 and get .5m(d/t)^2 + mgy1 = .5m(d/t)^2 since the velocity is the same at the bottom and top of the ramp?

 

[Dick]

Energy can easily get you the velocity over the flat L-D stretch of the ramp. So that time is just L-D over that velocity. You want to add that to the ramp time. Here you'll just have to use kinematics. Figure out the component of acceleration down the ramp and use that to get the time to descend the ramp. Now add the two times and find a minimum by taking a derivative with respect to D.

 

[NAkid]

I think I understand your logic but I still have a few questions--

Energy can easily get you the velocity over the flat L-D stretch of the ramp. So that time is just L-D over that velocity.

I'm assuming here I'll use work-energy theorem for straight-line motion?
.5mv1^2 - .5mv2^2

What do I do with mass? And how does time=(L-D)/v ?

 

[Dick]

It's moving at a CONSTANT velocity over the flat part of the track. time=distance/velocity.

 

[NAkid]

ok that makes sense.

now for the time on the ramp. the distance is (H^2 + D^2)^.5. can this distance be thought of as the displacement?

 

[Dick]

It can not only be thought of as the displacement, it IS the displacement. This part of the problem is a simple inclined plane problem. It's not rocket science.

 

[NAkid]

thanks...dick.

 

[Dick]

Touche. I can get abrupt and impatient this time of night when these things drag out, apologies. You can handle this. Compute the acceleration down the incline and use the displacement we both agree on, and find the time.