leprofece
- 239
- 0
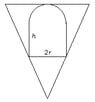
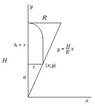
In a cone circular line of 15 cm in height and radius 5 cm fits a body cylindrical topped by 1 hemisphere tangent to the base of the cone. Calculate the height and radius of Ia part cylindrical if the volume of the registered body is the largest possible
Answer R = H = 3 cm
V= pir^2h/3 cone
V Hemisfere = 2pir^3/3
I don't know how to solve h if in the other there is no H
Answer R = H = 3 cm
V= pir^2h/3 cone
V Hemisfere = 2pir^3/3
I don't know how to solve h if in the other there is no H