What is the Polarization of These Waves?

[fluidistic]

Homework Statement

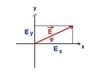
The question reads "What is the polarization of the following waves?"
1)$$\vec E = E_0 [\hat i \cos (\omega t - kz) + \hat j \cos (\omega t - kz + \frac{5 \pi}{4}) ]$$.
2)$$\vec E = E_0 [\hat i \cos (\omega t + kz) + \hat j \cos (\omega t + kz - \frac{ \pi}{4}) ]$$.
3)$$\vec E = E_0 [\hat i \cos (\omega t - kz) - \hat j \cos (\omega t - kz + \frac{ \pi}{6}) ]$$.

Homework Equations

No idea.

The Attempt at a Solution

I've checked out the magnitude of $$\vec E$$ in the 3 cases and it's never constant. Thus I'm guessing the 3 expressions represent elliptical polarizations. By pure guess, 1) and 2) are right polarized and 3) is left polarized.

Also I've no idea what they want me to do. I don't understand what they want by "what is the polarization". Is it "characterize mathematically the polarization"?
What equation should I use?

 

[ehild]

Characterize the state of polarization of the waves. You are right, they are elliptically polarized. To find if they represent right-screw or left screw, try to plot the electric field at a point at time t=0 and a bit later and see the turning direction with respect to the direction of travel.

ehild

 

[fluidistic]

Thanks, I appreciate your help.
When you say

To find if they represent right-screw or left screw, try to plot the electric field at a point at time t=0 and a bit later and see the turning direction with respect to the direction of travel.

I have a problem with the bold part. For example for 1), in t=0 and z=0, $$\vec E=E_0 (\hat i + \cos ((5 \pi)/4) \hat j)$$ whlle at the same position but $$\frac{\pi}{2\omega}$$ s later, there's only a $$\hat j$$ component left. How do I know that in $$\frac{\pi}{2\omega}$$ s, the wave hasn't "turned" several times; in other words, how do I know that $$\frac{\pi}{2\omega}$$ s is "a bit later" and not "much later"?
If it is a bit later than I think that the E field turns clockwise, hence right-screw?
It would be the same for 2) since the wave goes in the opposite direction but the phase shift is inverted too, so it would make the same state of polarization.
And 3) would be left-screw polarized.

Is it possible to derive the equation of an ellipse from the values I have? If so, how?
Did I get the exercise right?

 

[ehild]

"A bit later" was meant less than pi/(2w).
If you prefer doing maths to drawing, , it is possible to give any two-dimensional vector with planar polar coordinates, r and φ.
Find the angle of E with respect to the x axis. Find the derivative of φ with respect to t at x=0 and t=0. The sign of the derivative shows the direction of rotation.

ehild

 

[fluidistic]

Thanks once again.
Yes, good idea about writing the expression in polar coordinates and then differentiate.
My only problem is translating the $$\hat i$$ into something of the form $$a \hat \theta + b \hat \phi$$.
I can't find how to do it on the Internet. Do you have an idea?

 

[americanforest]

Use these facts for conversion from polar to Cartesian and vice versa:

$$\hat{\theta}=-sin(\theta)\hat{x}+cos(\theta)\hat{y}$$

$$\hat{\rho}=cos(\theta)\hat{x}+sin(\theta)\hat{y}$$

$$sin(\theta)=\frac{y}{\sqrt{x^{2}+y^{2}}}$$

$$cos(\theta)=\frac{x}{\sqrt{x^{2}+y^{2}}}$$

Solve this system of equations for the Cartesian unit vectors if you're interested.

Also, a short time later is any time such that the argument has not advanced through a full revolution (i.e. it has gone through less than $$2 \pi$$). If you increment time by the amount you mentioned then the argument of the trig functions gets incremented by

$$\frac{\pi}{2 \omega} \omega < 2 \pi$$

so you're safe.

 

[fluidistic]

Use these facts for conversion from polar to Cartesian and vice versa:

$$\hat{\theta}=-sin(\theta)\hat{x}+cos(\theta)\hat{y}$$

$$\hat{\rho}=cos(\theta)\hat{x}+sin(\theta)\hat{y}$$

$$sin(\theta)=\frac{y}{\sqrt{x^{2}+y^{2}}}$$

$$cos(\theta)=\frac{x}{\sqrt{x^{2}+y^{2}}}$$

Solve this system of equations for the Cartesian unit vectors if you're interested.

Hey thanks a lot, I appreciate your help. I have a few questions.
First, how do you derive those versors? Second, I needed $$\hat i$$ (or your $$\hat x$$) in terms of $$\hat \rho$$ and $$\hat \theta$$ and since you said "and vice versa", I guess I can get what I want, but I don't see how.

Also, a short time later is any time such that the argument has not advanced through a full revolution (i.e. it has gone through less than $$2 \pi$$). If you increment time by the amount you mentioned then the argument of the trig functions gets incremented by

$$\frac{\pi}{2 \omega} \omega < 2 \pi$$

so you're safe.

Ok I get that.
I find the polar coordinates and specially the sign of the derivative of $$\theta$$ to be an awesome idea. So I'd like to stick with it instead of Cartesian coordinates.

 

[americanforest]

Just replace the cosines and sines in the first two equations with the expressions in terms of x and y from the last two equations. Then solve the two first equations for your two unknowns, the Cartesian unit vectors.

This will give you the unit vectors as functions of x and y. If you want them in terms of the polar coordinates just use

$$x=\rho cos(\theta)$$

$$y=\rho sin(\theta)$$

I'm not going to go through the derivation of polar unit vectors but its very simple and I'm sure a quick Google search will lead you to something helpful.

 

[ehild]

Thanks once again.
Yes, good idea about writing the expression in polar coordinates and then differentiate.
My only problem is translating the $$\hat i$$ into something of the form $$a \hat \theta + b \hat \phi$$.
I can't find how to do it on the Internet. Do you have an idea?

Why don't you draw the vector in the x,y plane? It has x and y coordinates, and magnitude and angle as well. See attachment. How do you get the angle φ from the x, y coordinates? How would you get the magnitude of the vector?

The polar coordinates are the magnitude of the vector and its angle (the polar angle) with respect to a specified direction. The unit vectors are r -hat and φ-hat.
http://en.wikipedia.org/wiki/Polar_coordinate_system

ehild