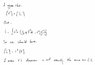- #1
shadi_s10
- 89
- 0
Dear all,
I am reading some texts about quintessence. As you one of the best textbooks for cosmology is Weinberg's. in page 90 of his book he states that if we consider astronomical units we can see that a good quintessence potential is
V([tex]\phi[/tex])= (M^(4+alpha)) * phi ^(-alpha)
and M has the dimention of mass.
Can anyone tell me if we do not work in that unit (I mean we do not consider h=c=1) what would exactly the potential be?
please help!
I really need to know this...
I am reading some texts about quintessence. As you one of the best textbooks for cosmology is Weinberg's. in page 90 of his book he states that if we consider astronomical units we can see that a good quintessence potential is
V([tex]\phi[/tex])= (M^(4+alpha)) * phi ^(-alpha)
and M has the dimention of mass.
Can anyone tell me if we do not work in that unit (I mean we do not consider h=c=1) what would exactly the potential be?
please help!
I really need to know this...