James1238765
- 120
- 8
- TL;DR Summary
- How to calculate numerical probabilities using Feynman diagram?
I have seen many tutorials that provide steps how to transcribe a Feynman diagram into algebra, for instance [here]:
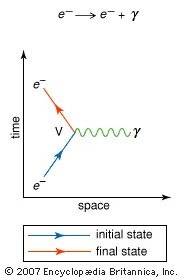
However, I have never seen the final line of the calculation converted into a real number. What are the steps to get from the algebra equations transcribed using the Feynman diagram, into a final concrete (eg 0.1726341) probability number for this interaction to happen?
However, I have never seen the final line of the calculation converted into a real number. What are the steps to get from the algebra equations transcribed using the Feynman diagram, into a final concrete (eg 0.1726341) probability number for this interaction to happen?