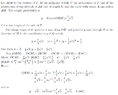lfdahl
Gold Member
MHB
- 747
- 0
A point $P$ is chosen at random with respect to the uniform distribution in an
equilateral triangle $T$. What is the probability that there is a point $Q$ in $T$ whose distance
from $P$ is larger than the altitude of $T$?
equilateral triangle $T$. What is the probability that there is a point $Q$ in $T$ whose distance
from $P$ is larger than the altitude of $T$?