- #1
sid_galt
- 502
- 1
I am a novice at stress analysis. For my competition, I need to calculate the stress on a torus in vacuum filled with air at pressure P.
Here's is what I have managed to do. I have attached an image below.
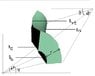
The torus section is an angular section of a curved cylinder. Its angular dimensions are d\psi in reference to the torus cross section at an angle \psi to the horizontal and d\theta in reference to the center of the torus. The major radius of the torus is R and the minor Radius is r.
Summing the forces in the radial direction
<br /> \displaystyle\frac{1}{2}(r+dr)d\psi[R-rcos(\psi+d\psi)+R-rcos\psi]d\theta*\sigma_r - \displaystyle\frac{1}{2}dr[R-rcos(\psi+d\psi)+R+drcos\psi-rcos(\psi+d\psi)]d\theta*\sigma_{t1}+\displaystyle\frac{1}{2}\pi[(r+dr)^2-r^2]d\theta*\sigma_{t2}=0<br />
Here \sigma_{t1} is the tangential stress with reference to the cross section of the torus and \sigma_{t2} is the tangential stress with reference to the center of the torus and \sigma_r is the radial stress.
<br /> \displaystyle\frac{1}{2}(r+dr)d\psi[R-rcos(\psi+d\psi)+R-rcos\psi]d\theta is the area between R_{rt} and R_{rb}(See figure)
<br /> \displaystyle\frac{1}{2}dr[R-rcos(\psi+d\psi)+R+drcos\psi-rcos(\psi+d\psi)]d\theta is the area between R_{rt} and R_{lt}
Am I correct upto this point? If I am, how do I process further?
Here's is what I have managed to do. I have attached an image below.
The torus section is an angular section of a curved cylinder. Its angular dimensions are d\psi in reference to the torus cross section at an angle \psi to the horizontal and d\theta in reference to the center of the torus. The major radius of the torus is R and the minor Radius is r.
Summing the forces in the radial direction
<br /> \displaystyle\frac{1}{2}(r+dr)d\psi[R-rcos(\psi+d\psi)+R-rcos\psi]d\theta*\sigma_r - \displaystyle\frac{1}{2}dr[R-rcos(\psi+d\psi)+R+drcos\psi-rcos(\psi+d\psi)]d\theta*\sigma_{t1}+\displaystyle\frac{1}{2}\pi[(r+dr)^2-r^2]d\theta*\sigma_{t2}=0<br />
Here \sigma_{t1} is the tangential stress with reference to the cross section of the torus and \sigma_{t2} is the tangential stress with reference to the center of the torus and \sigma_r is the radial stress.
<br /> \displaystyle\frac{1}{2}(r+dr)d\psi[R-rcos(\psi+d\psi)+R-rcos\psi]d\theta is the area between R_{rt} and R_{rb}(See figure)
<br /> \displaystyle\frac{1}{2}dr[R-rcos(\psi+d\psi)+R+drcos\psi-rcos(\psi+d\psi)]d\theta is the area between R_{rt} and R_{lt}
Am I correct upto this point? If I am, how do I process further?
Attachments
Last edited:
Out of curiosity, have you reviewed the solution for a straight pipe or spherical vessel. That should give you an idea the basic theory.
