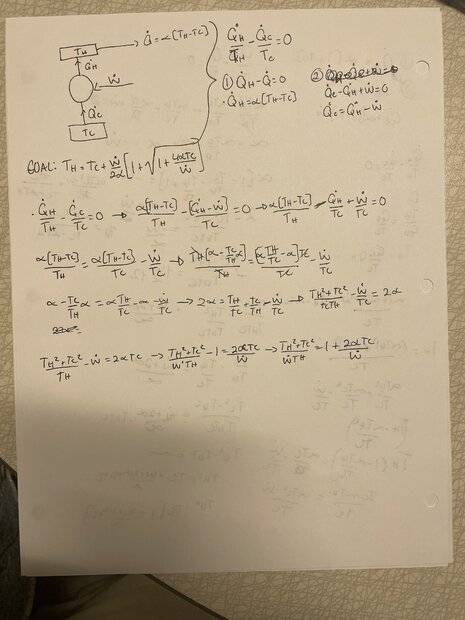- #1
guyvsdcsniper
- 264
- 37
- Homework Statement
- A building is maintained at temperature
TH with a reversible heat pump operating between the building and a
colder environment at temperature TC < TH. The heat pump consumes electrical
power at a constant rate W . The building also loses heat according to
Newton’s law of cooling, that is, at a rate (TH – TC) where is constant.
Show that the building temperature is maintained at temperature
- Relevant Equations
- dQrev/T = 0
I have went about this problem many different ways but cannot seem to come up with the answer. I am essentially trying to prove the formula provided in the ss of the problem.Could someone help me and tell me if I am approaching this wrong?