- #1
Jameson
Gold Member
MHB
- 4,541
- 13
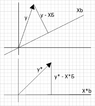
Problem: Through transformation with orthogonal matrix $O$, the problem \(\displaystyle \hat{b}=\underset{b}{\operatorname{arg min}}||y-Xb||^2\) is equivalent to \(\displaystyle \hat{b}=\underset{b}{\operatorname{arg min}}||y^{*}-X^{*}b||^2\), where $y$ and $y^{*}$ are in $\mathbb{R}^m$, $X$ and $X^{*}$ are in $\mathbb{R}^{m \times n}$ ($m \ge n$) and $y^{*}=Oy$ and $X^{*}=OX$. Let $y^{*}=[y_1^{*},y_2^{*}...,y_m^{*}]^T$.
Prove that the residual sum of square \(\displaystyle ||y-X \hat{b}||^2=\sum_{i=n+1}^{m}||y_i^{*}||^2\).
Solution: I must admit I am a bit overwhelmed by this problem. I believe that $\underset{b}{\operatorname{arg min}}$ just means "for the lowest value of $b$", correct? I think I should start by reading up on the concepts which are needed to solve this. Can someone highlight the main ideas I'll need to know to attack this?
Prove that the residual sum of square \(\displaystyle ||y-X \hat{b}||^2=\sum_{i=n+1}^{m}||y_i^{*}||^2\).
Solution: I must admit I am a bit overwhelmed by this problem. I believe that $\underset{b}{\operatorname{arg min}}$ just means "for the lowest value of $b$", correct? I think I should start by reading up on the concepts which are needed to solve this. Can someone highlight the main ideas I'll need to know to attack this?