What is the rate of change of angle in a 90 degree triangle?

[ardentmed]

Hey guys,

I need some more help for this problem set I've been working on. I'm doubting some of my answers and I'd appreciate some help.

This is only for question 1. Ignore 2.
Question:

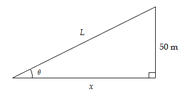
For the first one, drawing out the question clearly tells us that we are working with a 90 degree triangle. Thus, we can calculate the angle via cosØ and the Pythagorean formula.

The derivative thereof is:

-sinØ dØ/dt = [dx/dt (s) - ds/dt (x)] / s^2

We can substitute for values and solve for ds/dt, which leads to:

ds/dt = 1.73205 m/s (is this supposed to be an exact value?


Thus, dØ/dt can be calculated via substitution of the newly calculated ds/dt value. From isolation, we get:

dØ/dt = -0.055 m/s (or decreasing at a rate of 0.055 m/s. I'm highly doubtful of my response to this question.

Thanks in advance.

 

[MarkFL]

Beginning with a sketch is a very good first step:

View attachment 2841

As we can see, we may write:

$$\cot(\theta)=\frac{x}{50}$$

Now, if we implicitly differentiate with respect to time $t$, we get:

$$-\csc^2(\theta)\d{\theta}{t}=\frac{1}{50}\d{x}{t}$$

Now, since:

$$\csc(\theta)=\frac{L}{50}$$

we may write:

$$\d{\theta}{t}=-\frac{50}{L^2}\d{x}{t}$$

Now, what do you get when you plug in the given values for $$L,\,\d{x}{t}$$?

 

[ardentmed]

Beginning with a sketch is a very good first step:

View attachment 2841

As we can see, we may write:

$$\cot(\theta)=\frac{x}{50}$$

Now, if we implicitly differentiate with respect to time $t$, we get:

$$-\csc^2(\theta)\d{\theta}{t}=\frac{1}{50}\d{x}{t}$$

Now, since:

$$\csc(\theta)=\frac{L}{50}$$

we may write:

$$\d{\theta}{t}=-\frac{50}{L^2}\d{x}{t}$$

Now, what do you get when you plug in the given values for $$L,\,\d{x}{t}$$?

Plugging in the aforementioned values results in the following expression:

$\d{\theta}{t}$ = (-50*2)/(100^2)
$\d{\theta}{t}$ = -1/100 rad/minute (albeit I'm doubting the units for the final answer. Is it m/s, since the other units were also m/s? I just assumed rad/minute due to commonly seeing it used in related rates questions with angles.)

Thanks again.

 

[MarkFL]

Yes, the angle is decreasing at a rate of 1/100 rad/s at that point in time. If you look at the right side of:

$$\d{\theta}{t}=-\frac{50}{L^2}\d{x}{t}$$

Performing a dimensional analysis, we see the units are:

$$\frac{\text{m}}{\text{m}^2}\cdot\frac{\text{m}}{\text{s}}=\frac{1}{\text{s}}$$

Because we measure angles in radians, and being the ratio of two lengths, are dimensionless, so we take the rate of change here to be radians per second.