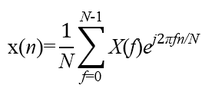- #1
maysam1
- 3
- 0
Suppose that there is a linear relation between discrete time (n) and frequency (f), then what is the relatian between x(n) and X(f) (X(f) is DFT transform of x(n))?
Last edited: