- #1
What is the relationship between a vector and a plane in terms of parallelism?
In summary, the conversation discusses the concept of parallel planes and how vectors b and c are parallel to a plane. The person asking for clarification is having trouble understanding this concept and asks for a better diagram. The person explaining uses the analogy of a sheet of paper and connecting points on it to explain how vectors can be parallel to a plane.
![DSC_0001~8~2[1].jpg](/data/attachments/53/53885-6609e8ddcfebb400cedbdf58bdc5773a.jpg)
- #2
jedishrfu
Mentor
- 15,106
- 9,632
first if you take two lines that aren't parallel and that intersect at some point a then visually you should agree that there is a plane that contains the two lines and the intersection point. right?
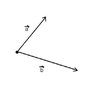
well vector b is along the first line and vector c is along the second line and a is the point in the plane.
well vector b is along the first line and vector c is along the second line and a is the point in the plane.
Last edited:
- #3
kelvin macks
- 60
- 0
jedishrfu said:
i can only imagine and say vector b and vextor c contain in the same plane. why both vector are parallel to the plane? i can't understand
- #4
ehild
Homework Helper
- 15,542
- 1,917
b and c are vectors lying on the the plane. Take a sheet of paper, draw two vectors on it, like b and c in the first figure.
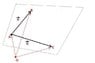
Lift the paper. It is a piece of a plane (second figure). Choose a point as origin somewhere outside the plane (O), and connect it to A, B, C. ##\vec {OA}##, ##\vec {OB}##, ##\vec {OC}## are the position vectors pointing to A, B, C, points of the plane .
ehild
Lift the paper. It is a piece of a plane (second figure). Choose a point as origin somewhere outside the plane (O), and connect it to A, B, C. ##\vec {OA}##, ##\vec {OB}##, ##\vec {OC}## are the position vectors pointing to A, B, C, points of the plane .
ehild
Attachments
- #5
kelvin macks
- 60
- 0
ok i can uderstanf it better now .
FAQ: What is the relationship between a vector and a plane in terms of parallelism?
What is the equation for a plane in vector form?
The equation for a plane in vector form is r = r0 + s1v1 + s2v2, where r0 is a point on the plane, v1 and v2 are two independent vectors in the plane, and s1 and s2 are scalar parameters.
How do you find the normal vector of a plane?
The normal vector of a plane can be found by taking the cross product of two non-parallel vectors in the plane. This will result in a vector that is perpendicular to both of the original vectors and is therefore normal to the plane.
Can a plane be defined by only one vector?
No, a plane cannot be defined by only one vector. A plane requires at least two independent vectors to be fully defined. This is because a single vector only provides information about direction, not position.
How do you determine if a point lies on a plane?
A point lies on a plane if its position vector, r, satisfies the plane equation r = r0 + s1v1 + s2v2, where r0 is a point on the plane and v1 and v2 are two independent vectors in the plane. To check if a point satisfies this equation, you can substitute its coordinates into the equation and see if it holds true.
How is a plane represented in 3D space?
A plane is represented in 3D space by a flat, two-dimensional surface that extends infinitely in all directions. It is typically represented by a geometric shape called a parallelogram or by its equation in vector form.