What Is the Relationship Between Radiant Intensity and Radiance?

[spacediver]

Hi all, been a while since I've posted here, but figured this would be a great place to ask this question.

I've gone over the first chapter of McCluney's Introduction to Radiometry a number of times, and more recently have discovered this great resource, but I am still confused about something.

For the purposes of this discussion, I'm reducing the number of spatial dimensions by one. So instead of solid angle (in steradians), I'll be using angle (in radians), and instead of area (in m²), I'll be using length (in m). This is done with the full understanding that in reality, light propagates in all three spatial dimensions and intersects surfaces and not lines. Nevertheless, I believe it's useful to simplify things here.

Take a look at this figure:

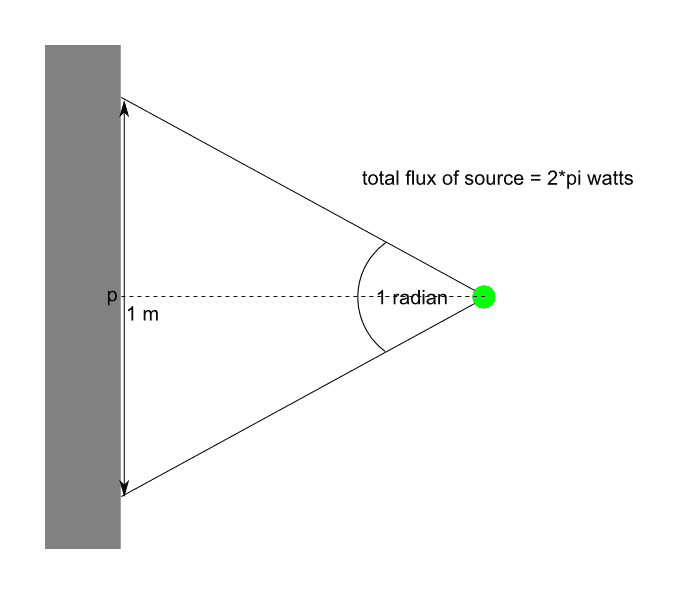
On the left is a surface receiving light from a point source on the right.

The total flux of the source is 2 pi watts, and we will assume that the angular distribution of flux is uniform, which means that the radiant intensity, as measured as exitant from the point source is uniform across all directions.

Given the above, we can now say that the amount of flux contained within the depicted angle is one watt (2*pi watts divided by 2*pi radians). This means that the radiant intensity exitant from the point source is exactly one watt/radian, and this radiant intensity is the same in all directions.

We can also say that the amount of flux incident upon the depicted length of the surface on the left is exactly one watt.

First question: Have I got this right so far?

My next question has to do with calculus, which I have a very tenuous grasp of.

I understand that radiometric quantities are defined with respect to infinitesimals, and the partial, or elemental length of the surface on the left does not scale linearly with the partial angle subtended, so we can't say that the irradiance upon the surface at point P is one watt per metre. For instance, if we reduced our angle to half a radian, the length "covered" by this angle would be smaller than half a meter. Thus, as the angle gets smaller, the covered length becomes smaller at a greater rate. Thus, the flux density upon the elemental length becomes greater and greater as the angle approaches 0. Accordingly, the irradiance at point P is quite a bit greater than 1 watt/m. I lack the calculus know how to be able to figure out the derivative, but I'm guessing it has something to do with the derivative of tan theta, where theta is the angle in question.

Second question: Is the above paragraph on the right track, and how would one go about figuring out the irradiance at point P that is due to the light source?

Now onto the next part of my confusion.

Suppose that the irradiance at point P, due to the point source, is X watts/m.

Would the radiance at point P, due to the point source, be X watts/m/radian?

If so, then why on Earth is this a useful quantity? What does radiance tell you couldn't figure out from radiant intensity? I thought radiant intensity, irradiance, and radiance were all fundamental quantities. That to me suggests some form of independence, kind of like mass and velocity are independent properties of an object. Yet if I'm understanding this correctly, one can figure out the radiance just by knowing the radiant intensity, and the distance from an object. Why is this useful? I remember reading something about how radiance is distance independent - i.e. the radiance of a source does not depend on the distance from the source to the target surface.

I have a feeling I'm missing something ridiculously obvious, and this has been bugging me for quite a while!

Finally, I kinda get that we can talk about these quantities both with respect to exitance and incidence. So in this example, assuming I was correct, the radiance at point P, due to the point source, is X watts per radian. Could we also talk about the radiance of the point source? Or could we only do that if the source of light was a surface extended in space?

I'd greatly appreciate any insights here!

 

[UltrafastPED]

This summary of terms may be helpful: http://www.astrohandbook.com/ch14/radiation_defs.pdf

 

[spacediver]

thanks I'll try to read that tonight when I get home.

 

[elegysix]

The total flux of the source is 2 pi watts, and we will assume that the angular distribution of flux is uniform, which means that the radiant intensity, as measured as exitant from the point source is uniform across all directions.

yes

Given the above, we can now say that the amount of flux contained within the depicted angle is one watt (2*pi watts divided by 2*pi radians). This means that the radiant intensity exitant from the point source is exactly one watt/radian, and this radiant intensity is the same in all directions.

$\frac{2\pi \text{ W}}{2 \pi \text{ radians}}\times \text{ 1 radian} = 1 \text{ W}$
But yes 1 W/ radian is the radiant intensity (usually W/radian^2 or W/sr )

I understand that radiometric quantities are defined with respect to infinitesimals, and the partial, or elemental length of the surface on the left does not scale linearly with the partial angle subtended, so we can't say that the irradiance upon the surface at point P is one watt per metre. For instance, if we reduced our angle to half a radian, the length "covered" by this angle would be smaller than half a meter. Thus, as the angle gets smaller, the covered length becomes smaller at a greater rate. Thus, the flux density upon the elemental length becomes greater and greater as the angle approaches 0. Accordingly, the irradiance at point P is quite a bit greater than 1 watt/m. I lack the calculus know how to be able to figure out the derivative, but I'm guessing it has something to do with the derivative of tan theta, where theta is the angle in question.

You are right that the irradiance at different points along the surface will be different. This is because the irradiance from a point source follows an inverse square law, and different points along the surface are at different distances from the source. However, for the total surface the average value of 1 W/m (or W/m^2 in 3 dimensions) is true. If your surface were a sphere centered on the source, the value of irradiance would indeed be the same at each point as the average value.

I've been working on a project involving the solar spectra and light bulb spectra for the last year. The terminology can get very confusing to a reader. I recommend sticking to Irradiance (W/m^2) and Spectral Irradiance (W/m^2/nm or W/m^3) aka spectral power density. Intensity by itself is very loosely used when it comes to these quantities, and can be a point of confusion. Unless there's a special need to involve units of radians or steridians, I would stay away from it.

 

[spacediver]

Thanks very much for the reply elegysix :)

If your surface were a sphere centered on the source, the value of irradiance would indeed be the same at each point as the average value.

Here's a revamped figure, so now we can safely say that the irradiance incident at point P is 1 Watt/m.

I've been working on a project involving the solar spectra and light bulb spectra for the last year. The terminology can get very confusing to a reader. I recommend sticking to Irradiance (W/m^2) and Spectral Irradiance (W/m^2/nm or W/m^3) aka spectral power density. Intensity by itself is very loosely used when it comes to these quantities, and can be a point of confusion. Unless there's a special need to involve units of radians or steridians, I would stay away from it.

Yep I'm aware of the multiple usage of the term intensity. I'm using radiant intensity in the radiometric sense, and am not worrying for now about other usages of the term. I feel that I need to have a solid grasp of the concept of radiant intensity and irradiance in order to fully grok radiance, which is why I'm using it in this example to build up my understanding.

With that said, how exactly would you calculate the radiance, incident upon point P, due to the point light source?

In my reduced dimensionality scenario, we know that the incident irradiance at point P, due to the point light source, is 1 Watt/m. We also know that the radiant intensity exitant from the point light source is 1 Watt/radian. So how do we calculate the radiance incident upon point P?

 

[elegysix]

In my reduced dimensionality scenario, we know that the incident irradiance at point P, due to the point light source, is 1 Watt/m. We also know that the radiant intensity exitant from the point light source is 1 Watt/radian. So how do we calculate the radiance incident upon point P?

Apparently i wasn't thinking straight when I posted last. The average value of irradiance, is the power emitted through the angle, 1W, divided by the length (usually area) it is incident on. So if the rectangular object has a length L within the angle, then the average irradiance will be 1/L W/m, not 1 W/m.

For the semicircle, since all points are equidistant from the source, we know the value at any point must be the same as all the others. that's why the average value of irradiance is the value at each point.

here's a link which might help you understand the calculations

 

[spacediver]

thanks, but I'm still unclear on how to calculate the radiance at point P. (I'm pretty comfortable with irradiance and radiant intensity, but radiance is what I'm struggling with).

 

[elegysix]

I don't think it makes sense to talk about radiance at a point, since radiance depends on a solid angle and surface area. That's why I only brought up irradiance at P.

I suppose it could make sense if we were talking about a large emitter, (not a point source), but this is about the limit of my knowledge on it.

 

[spacediver]

I don't think it makes sense to talk about radiance at a point, since radiance depends on a solid angle and surface area. That's why I only brought up irradiance at P.

I suppose it could make sense if we were talking about a large emitter, (not a point source), but this is about the limit of my knowledge on it.

That's what I would have thought, but apparently radiance can be defined at a point.

See figure 6 on this page.

Also consider the definition of radiance (from McCluney's text):

Radiance, L, is the area and solid angle density of radiant flux, the radiant flux per unit projected area and per unit solid angle incident on, passing through, or emerging in a specified direction from a specified point in a specified surface...

bold emphasis mine.

 

[elegysix]

Ok from figure 6 you will notice that the point P is the source, not on the surface element. So that should help clear some things up. It seems like to calculate radiance, we have to work the problem backwards from what we were doing. start with the power incident on the surface, and solve for the power radiated and the angle.

 

[spacediver]

yep, fig 6 is depicting radiance at a point source, but the definition I quoted seems to indicate a "recipient" point.

Furthermore, from the "www.scratchapixel.com/lessons/3d-basic-lessons/lesson-15-introduction-to-shading-and-radiometry/introduction-to-radiometry-2/" :

It is important to remember that radiance applies to both light arriving (incident on) at a point on the surface as well as to light leaving (emerging from) a given point on a surface and traveling in any given direction in the hemisphere oriented about the surface normal at that point. What works for incident light also work for light reflected from x to any direction in the sphere; all you need to do is just flip the direction. We have illustrated this idea with two different figures (13 and 14).

 

[elegysix]

Ok. I think I know the problem. You can't calculate radiance at a point, from a point source.
One side can be a point, but the other must be a surface. This is because there's no area or angle between two points. But I'm just guessing now. I'm not familiar enough with radiance. Sorry I couldn't be of better help on your quest

 

[spacediver]

thanks, that makes sense. Really appreciate your input here - you've definitely guided me further along my quest :)

I'll certainly report back in this thread if and when I figure this infernal situation out!

 

[spacediver]

I might be starting to understand radiance, thanks to this document (in particular page 4).

When we consider the definition of irradiance, we are considering the area density of flux, when considering the whole hemisphere.

I think radiance is simply the same thing but considering a single steradian of solid angle, rather than the whole hemisphere (2 pi steradians).

The usefulness of this is that, barring any loss of light energy along the path of travel (e.g. atmospheric absorption), radiance remains constant, since it is a measure that expresses the proportionality between angle and area.

I'll try to wrap my head around this and figure out a diagram or something soon. I'm not even sure that this understanding is correct yet.