- #1
Bruce_Pipi121
- 9
- 4
- Homework Statement
- Consider two sound waves travelling with the same speed and amplitude but having similar but slightly different wavelengths, ##λ_1## and ##λ_2##, and angular frequencies, ##ω_1## and ##ω_2##. The two waves are described with the functions $$y_1 (x,t) = A cos (\frac{2\pi x}{\lambda_1}- \omega_1 t)$$ $$y_2 (x,t) = A cos (\frac{2\pi x}{\lambda_2}- \omega_2 t)$$
a) What is the speed v in terms of the angular frequencies and wavelengths?
b) Sketch y1 + y2 as a function of x, at some time t.
c) If you stood in the path of these sound waves, what frequency would you hear (assuming you can hear it)?
d) What is the distance between points where the sound disappears?
- Relevant Equations
- $$cos x +cos y = 2 cos{\frac{x+y}{2}}cos{\frac{x-y}{2}}$$
for a) I have ##v = \lambda f= \frac{\omega \lambda}{2 \pi}##
for c) and d) I denote ##\frac{2\pi}{\lambda_1} = k_1## and ##\frac{2\pi}{\lambda_2} = k_2## assuming ##k_1 > k_2##.
so using the triangular identity I got $$y_1 + y_2 = 2A cos(\frac{k_1+k_2}{2} x - \frac{\omega_1 + \omega_2}{2} t) cos(\frac{k_1-k_2}{2} x - \frac{\omega_1 - \omega_2}{2} t)$$
To simplify the equation I denote ##K_1 = \frac{k_1+k_2}{2}##, ##K_2 = \frac{k_1-k_2}{2}##, ##\Omega_1 = \frac{\omega_1+\omega_2}{2}## and ##\Omega_2 = \frac{\omega_1 - \omega_2}{2}##, so $$y_1 + y_2= 2A cos(K_1 x - \Omega_1 t)cos(K_2 x - \Omega_2 t)$$ and since ##k_1 \approx k_2 ## so ##K_1 >> K_2## and ##\omega_1 \approx \omega_2 ## so ##\Omega_1 >> \Omega_2##
now from the graph I can solve for d) distance is ##\frac{\pi}{K_2}##
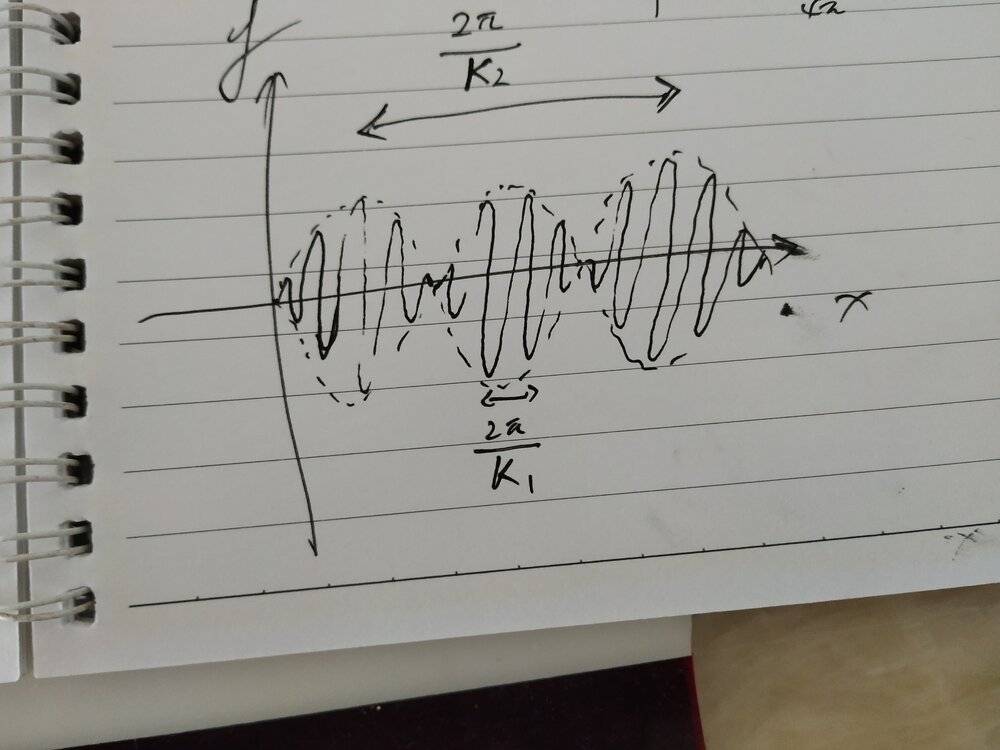
but I am not sure about c) is the frequency we would hear is ##f = \frac{\Omega_1}{2 \pi}##, why?
for c) and d) I denote ##\frac{2\pi}{\lambda_1} = k_1## and ##\frac{2\pi}{\lambda_2} = k_2## assuming ##k_1 > k_2##.
so using the triangular identity I got $$y_1 + y_2 = 2A cos(\frac{k_1+k_2}{2} x - \frac{\omega_1 + \omega_2}{2} t) cos(\frac{k_1-k_2}{2} x - \frac{\omega_1 - \omega_2}{2} t)$$
To simplify the equation I denote ##K_1 = \frac{k_1+k_2}{2}##, ##K_2 = \frac{k_1-k_2}{2}##, ##\Omega_1 = \frac{\omega_1+\omega_2}{2}## and ##\Omega_2 = \frac{\omega_1 - \omega_2}{2}##, so $$y_1 + y_2= 2A cos(K_1 x - \Omega_1 t)cos(K_2 x - \Omega_2 t)$$ and since ##k_1 \approx k_2 ## so ##K_1 >> K_2## and ##\omega_1 \approx \omega_2 ## so ##\Omega_1 >> \Omega_2##
now from the graph I can solve for d) distance is ##\frac{\pi}{K_2}##
but I am not sure about c) is the frequency we would hear is ##f = \frac{\Omega_1}{2 \pi}##, why?