What is the shortest route to Gulch city?

[fatal1]

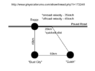
A dune buggy is on a straight desert road, 40 km north of Dust city. The vehicle can travel at 45 km/h off the road and 75 km/h on the road. The driver wants to go to Gulch city, 50 km east of Dust city in the shortest possible time. Determine the route he should take.

The equation i can up with to solve this is:

f(x) = .6(1600 + x^2)(2X) + (50 -x)

...I got the .6 by dividing 45 by 75 to get a ratio...what am I doing wrong? Please help, I have a test tomorrow and this is my last resort. Thanks.

edit: the answer is 30 km east of dust city but how?

 

[lalbatros]

Do I understand correctly?

The driver can decide to drive on the road a certain distance North-South.
Then he can leave the road and drive off road South-East.
The question does not specify if there is a road between Dust city and Gulch city.

I suggest you to calculate the travel time as a function of the driver decision(s).
If there is a road Dust-Gulch, then the driver should also decide about where to join this road.
Please make a drawing of this problem.

I solved the question as I could understand it, but I did not find the same solution.
Actually I even don't understand the solution: "30 km east of dust city", what does that mean, is there a road going east?
I even solved the question with a nothward road and an eastward road, and could not make sense of the answer.

So, the priority is make the statement of the problem clear.
Your equation too makes no sense for me, with my current understanding of the question.

 

[Timaxe]

Sorry to pull this month old thread back up (it also appears to have been posted in the wrong section too) but I came across this in my boredom today and felt like having a stab at it. But after solving it, I was was perplexed from being unable to find a useful constraint function.

To make sense of the OP's somewhat confusing description, I've attached a quick sketch that I threw together in Inkscape to layout what is going on.

...see attached image...

My objective function (time as a function of where to turn off the road) was [[ (x/75)+sqrt((40^2+(50-x)^2))/45 ]] and my solution involved simply plotting the points, and picking the point on the plot with the smallest value of time - corresponding to a turn off at 20km (30km before the city).

I can't help but think I skipped a step or something because I didn't come up with a useful constraint. I just want to minimize time...but shouldn't there be another constraint I can come up with that will let me solve this and get the answer x = 20km? If not, was this because I did something wrong/differently or is there another reason?

I'd like to look it up in my textbook to see how to properly do a regular/easy optimization problem so I could extend it to this problem to see where I went astray...but that's back at school and I'm already 5,000 miles away (overseas)... Can someone help me out? Thanks.