Devin-M
- 1,069
- 765
I've read the NIRCam instrument uses HgCdTe imaging sensors...
"JWST NIRCam has ten 2K × 2K HgCdTe detectors"
https://jwst-docs.stsci.edu/jwst-ne...rcam-instrumentation/nircam-detector-overview

I found this chart which displays the relative sensitivity of the NIRCam sensor for different filters and wavelengths:
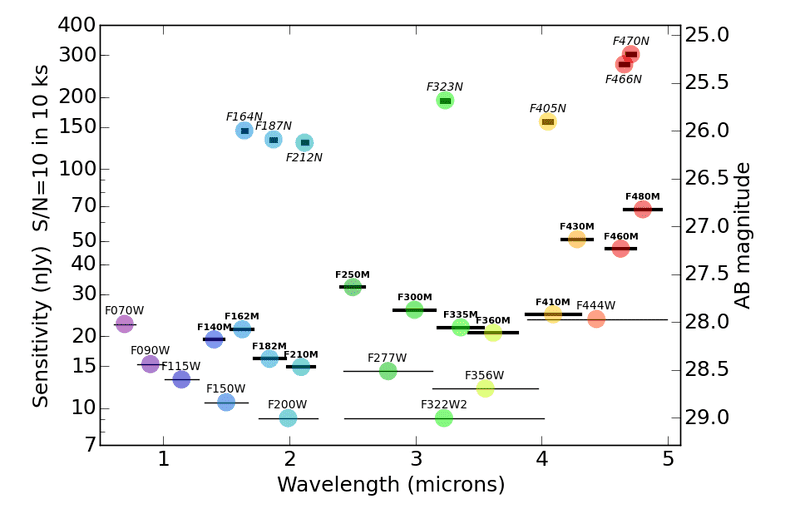
From the wikipedia article on Mercury Cadmium Telluride (HgCdTe) detectors:
"In HgCdTe, detection occurs when an infrared photon of sufficient energy kicks an electron from the valence band to the conduction band."
I tried to find a chart showing the "current responsivity" at different temperatures for the actual NIRCam sensor, but I couldn't locate one, so I pulled this chart from a paper written on a different HgCdTe photodiode which shows 1.6 amps per watt of 3.5 micron light incident on the sensor while the sensor is 300 Kelvin (would've posted the actual NIRCam specs if I could find them):
https://www.researchgate.net/publication/343856156_Higher_Operating_Temperature_IR_Detectors_of_the_MOCVD_Grown_HgCdTe_Heterostructures
https://www.speakev.com/cdn-cgi/image/format=auto,onerror=redirect,width=1920,height=1920,fit=scale-down/https://www.speakev.com/attachments/5000b9e5-011d-4ef0-af59-bedb15ff822e-jpeg.156575/
My question is this:
Considering that the 2nd Law of Thermodynamics is inviolable, and so the sensor shouldn't be able to "detect" an object which is colder than the imaging sensor, if the sensor above from figure 12 were used in NIRCam (since I can't find the actual NIRCam responsivity specs), what physical effect would prevent a 3.5 micron photon from kicking an electron from the valence band to the conduction band in the 300k sensor, if the photon were emitted as black body radiation from a 299k object? In other words, how would a valence electron in the sensor determine the temperature of the emitting object from the arriving 3.5 micron photon's characteristics such as wavelength before either being kicked or not kicked to the conduction band, in order to remain consistent with the 2nd Law?
"JWST NIRCam has ten 2K × 2K HgCdTe detectors"
https://jwst-docs.stsci.edu/jwst-ne...rcam-instrumentation/nircam-detector-overview
I found this chart which displays the relative sensitivity of the NIRCam sensor for different filters and wavelengths:
From the wikipedia article on Mercury Cadmium Telluride (HgCdTe) detectors:
"In HgCdTe, detection occurs when an infrared photon of sufficient energy kicks an electron from the valence band to the conduction band."
I tried to find a chart showing the "current responsivity" at different temperatures for the actual NIRCam sensor, but I couldn't locate one, so I pulled this chart from a paper written on a different HgCdTe photodiode which shows 1.6 amps per watt of 3.5 micron light incident on the sensor while the sensor is 300 Kelvin (would've posted the actual NIRCam specs if I could find them):
https://www.researchgate.net/publication/343856156_Higher_Operating_Temperature_IR_Detectors_of_the_MOCVD_Grown_HgCdTe_Heterostructures
https://www.speakev.com/cdn-cgi/image/format=auto,onerror=redirect,width=1920,height=1920,fit=scale-down/https://www.speakev.com/attachments/5000b9e5-011d-4ef0-af59-bedb15ff822e-jpeg.156575/
My question is this:
Considering that the 2nd Law of Thermodynamics is inviolable, and so the sensor shouldn't be able to "detect" an object which is colder than the imaging sensor, if the sensor above from figure 12 were used in NIRCam (since I can't find the actual NIRCam responsivity specs), what physical effect would prevent a 3.5 micron photon from kicking an electron from the valence band to the conduction band in the 300k sensor, if the photon were emitted as black body radiation from a 299k object? In other words, how would a valence electron in the sensor determine the temperature of the emitting object from the arriving 3.5 micron photon's characteristics such as wavelength before either being kicked or not kicked to the conduction band, in order to remain consistent with the 2nd Law?