- #1
danielakkerma
- 231
- 0
(Hello everyone!)
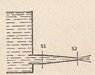
Water is gathered in a column of height h, above above a distributing pipe.
The pipe then narrows from cross sectional area S1 to S2(S1>S2), after which, the fluid exits(as shown in the attached figure)
Find the total horizontal force(in the direction of the fluid's flow) acting on the pipe.
(s1 = 3.0 cm^2, s2 = 1 cm^2, h = 4.6 m).
Bernoulli's law(dynamic pressure):
1. P = rho*v^2/2
The continuity equation 2. v1*s1=v2*s2=const.
I started by defining the force:
Over a certain, small, pressure drop, the (minute) force generated is:
[tex]dF = dP\cdot S(x) [/tex]
Where S(x) is cross-sectional area over the pressure gradient).
I assume that, before the pipe starts to constrict, as the fluid is taken to be ideal(inviscid), there are no force contributions there.
Therefore, according to Bernoulli, a small chance in pressure would be directly related to an alteration of the velocity, by differentiating 1.:
[tex] dP = \rho v dv [/tex]
And from continuity conditions:
[tex] S_1 v_1 = S(x)\cdot v(x) = const \\ v(x) = \frac{S_1 v_1}{S(x)} \\
dv = \frac{-S_1 v_1}{{S(x)}^2}dS \\
[/tex]
Plugging both into dF:
[tex] dF = dP\cdot S(x) = \rho vdv S(x) = -\rho\frac{S_1 v_1}{{S(x)}^2} \frac{S_1 v_1}{S(x)}S(x)dS = -\frac{\rho{S_1}^2{v_1}^2}{{S(x)}^2}dS [/tex]
Integrating, to obtain F, S, going from S1, to S2:
[tex] F = \rho {S_1}^2{v_1}^2 \int_{S_1}^{S_2}\frac{-dS}{{S^2}} = \rho {S_1}^2{v_1}^2 \cdot (\frac{1}{S_2}-\frac{1}{S_1}) [/tex]
Now, since v1 is the velocity the fluid gains from its column, i.e., due to gravity, Bernoulli gives us:
[tex] v_1 = \sqrt{2gh} [/tex]
Inserting all the given data gives me:
(rho is the density of water: 1 g/cm^3)
[tex] F \approx 55 N [/tex]
Yet the correct answer is, F = 6 N!
What have I done wrong?
Any help would be greatly appreciated,
And I am as always thankful for your time and attention,
Daniel
Homework Statement
Water is gathered in a column of height h, above above a distributing pipe.
The pipe then narrows from cross sectional area S1 to S2(S1>S2), after which, the fluid exits(as shown in the attached figure)
Find the total horizontal force(in the direction of the fluid's flow) acting on the pipe.
(s1 = 3.0 cm^2, s2 = 1 cm^2, h = 4.6 m).
Homework Equations
Bernoulli's law(dynamic pressure):
1. P = rho*v^2/2
The continuity equation 2. v1*s1=v2*s2=const.
The Attempt at a Solution
I started by defining the force:
Over a certain, small, pressure drop, the (minute) force generated is:
[tex]dF = dP\cdot S(x) [/tex]
Where S(x) is cross-sectional area over the pressure gradient).
I assume that, before the pipe starts to constrict, as the fluid is taken to be ideal(inviscid), there are no force contributions there.
Therefore, according to Bernoulli, a small chance in pressure would be directly related to an alteration of the velocity, by differentiating 1.:
[tex] dP = \rho v dv [/tex]
And from continuity conditions:
[tex] S_1 v_1 = S(x)\cdot v(x) = const \\ v(x) = \frac{S_1 v_1}{S(x)} \\
dv = \frac{-S_1 v_1}{{S(x)}^2}dS \\
[/tex]
Plugging both into dF:
[tex] dF = dP\cdot S(x) = \rho vdv S(x) = -\rho\frac{S_1 v_1}{{S(x)}^2} \frac{S_1 v_1}{S(x)}S(x)dS = -\frac{\rho{S_1}^2{v_1}^2}{{S(x)}^2}dS [/tex]
Integrating, to obtain F, S, going from S1, to S2:
[tex] F = \rho {S_1}^2{v_1}^2 \int_{S_1}^{S_2}\frac{-dS}{{S^2}} = \rho {S_1}^2{v_1}^2 \cdot (\frac{1}{S_2}-\frac{1}{S_1}) [/tex]
Now, since v1 is the velocity the fluid gains from its column, i.e., due to gravity, Bernoulli gives us:
[tex] v_1 = \sqrt{2gh} [/tex]
Inserting all the given data gives me:
(rho is the density of water: 1 g/cm^3)
[tex] F \approx 55 N [/tex]
Yet the correct answer is, F = 6 N!
What have I done wrong?
Any help would be greatly appreciated,
And I am as always thankful for your time and attention,
Daniel
Attachments
Last edited: