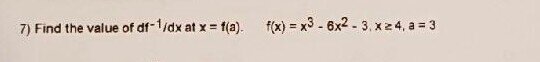What is the value of the inverse derivative at x=f(a)?

[karush]

find the value of $$df^{-1}/dx at $x=f(a)$$
$$f(x)=x^3-6x^2-3$$
$$x \ge 4$$
$$a=3$$

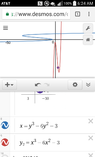
ok the inverse would be
$$x=y^3-6y^2-3$$

but don't see how to isolate $y$
or if we need to

 

[MarkFL]

First, I would verify that the given function is one-to-one on $[4,\infty)$. Then I recommend following these steps:

1.) Implicitly differentiation the following:

$$f(x)=x^3-6x^2-3$$

With respect to $f$ and solve for $$\d{x}{f}$$.

2.) Solve (I am assuming $a=-3$):

$$f(x)=-3$$

Call the relevant (must be real and in the stated domain) root $x_r$.

3.) Then we have:

$$\left[f^{-1}\right]'(a)=\left.\d{x}{f}\right|_{x=x_r}$$

 

[karush]

View attachment 7587
Original question

 

[MarkFL]

I'm thinking there's at least one typo in the problem...I think at the very least it should state:

$$x=f^{-1}(a)$$

Let's look at the standard formula:

$$\left[f^{-1}\right]'(a)=\frac{1}{f'\left(f^{-1}(a)\right)}$$

We know:

$$f\left(f^{-1}(a)\right)=a$$

Let:

$$u=f^{-1}(a)$$

And so we have:

$$f(u)=a$$

Using the given definition of $f$ and the given $a=3$, we have:

$$u^3-6u^2-3=3$$

As you can see, this would be much easier to solve if $a=-3$, but this can be solved. What do you get?

 

[karush]

I'm thinking there's at least one typo in the problem...I think at the very least it should state:

$$x=f^{-1}(a)$$

Let's look at the standard formula:

$$\left[f^{-1}\right]'(a)=\frac{1}{f'\left(f^{-1}(a)\right)}$$

We know:

$$f\left(f^{-1}(a)\right)=a$$

Let:

$$u=f^{-1}(a)$$

And so we have:

$$f(u)=a$$

Using the given definition of $f$ and the given $a=3$, we have:

$$u^3-6u^2-3=3$$

As you can see, this would be much easier to solve if $a=-3$, but this can be solved. What do you get?

what is $f^{-1}(a)$

 

[MarkFL]

what is $f^{-1}(a)$

Suppose we set:

$$f(x)=a$$

This is equivalent to:

$$x=f^{-1}(a)$$

This is what you'll find when solving:

$$x^3-6x^2-3=a$$

 

[karush]

this?

$\text{so if $a=3$ then}$
$\displaystyle x^3-6x^2-3=3$
$\displaystyle x^3-6x^2=6$
$\text{$x=6.1582$ \, via W|A}$

$\text{or if $a=-3$ then}$
$\displaystyle x^3-6x^2-3=-3$
$\displaystyle x^3-6x^2=0$
$x^2(x-6)=0$
$x=0$
$x=6$

 

[MarkFL]

this?

$\text{so if $a=3$ then}$
$\displaystyle x^3-6x^2-3=3$
$\displaystyle x^3-6x^2=6$
$\text{$x=6.1582$ \, via W|A}$

Yes, and the exact root is given as:

$$x=2+\sqrt[3]{11+\sqrt{57}}+\sqrt[3]{11-\sqrt{57}}$$

$\text{or if $a=-3$ then}$
$\displaystyle x^3-6x^2-3=-3$
$\displaystyle x^3-6x^2=0$
$x^2(x-6)=0$
$x=0$
$x=6$

We would discard the root $x=0$ since we are told $4\le x$. Can you demonstrate the given function is one-to-one on this interval?

At any rate, once we have the value of $f^{-1}(a)$, can you proceed?

 

[karush]

$\text{I'm not sure what $6.1582$ is supposed to plugged into}$

 

[MarkFL]

$\text{I'm not sure what $6.1582$ is supposed to plugged into}$

You could use this formula:

$$\left[f^{-1}\right]'(a)=\frac{1}{f'\left(f^{-1}(a)\right)}$$

where $a=3,\,f^{-1}(a)\approx6.1582$.

 

[karush]

You could use this formula:

$$\left[f^{-1}\right]'(a)=\frac{1}{f'\left(f^{-1}(a)\right)}$$

where $a=3,\,f^{-1}(a)\approx6.1582$.

$\displaystyle \left[f^{-1}\right]'(a)$
$=\frac{1}{f'\left(f^{-1}(a)\right)}$
$=\frac{1}{f'(6.1582)}$
$f'(6.1582)=3(6.11582)^2-12(6.11582)=38.8119$
$1/38.8119 =0.02576$

 

[MarkFL]

$\displaystyle \left[f^{-1}\right]'(a)$
$=\frac{1}{f'\left(f^{-1}(a)\right)}$
$=\frac{1}{f'(6.1582)}$
$f'(6.1582)=3(6.11582)^2-12(6.11582)=38.8119$

I get:

$$f'\left(f^{-1}(a)\right)\approx39.8722$$

W|A - (3(2 + (11 - sqrt(57))^(1/3) + (11 + sqrt(57))^(1/3))^2-12(2 + (11 - sqrt(57))^(1/3) + (11 + sqrt(57))^(1/3)))

And so:

$$\left[f^{-1}\right]'(a)\approx0.02508$$

W|A - 1/(3(2 + (11 - sqrt(57))^(1/3) + (11 + sqrt(57))^(1/3))^2-12(2 + (11 - sqrt(57))^(1/3) + (11 + sqrt(57))^(1/3)))

 

[DrWahoo]

I can post a graph of the function, derivative, inverse, and solution in graph forum from MATLAB if that helps anyone.

I must admit, the question is written in a very vague forum. It doesn't define everything how "most mathematicians" would. It leaves a lot of the problem open for interpretation.

 

[karush]

I can post a graph of the function, derivative, inverse, and solution in graph forum from MATLAB if that helps anyone.

I must admit, the question is written in a very vague forum. It doesn't define everything how "most mathematicians" would. It leaves a lot of the problem open for interpretation.

Sure
I did what I could with Desmos but
Could only do so much

 

[karush]

Over 100 views

 

[MarkFL]

Sure
I did what I could with Desmos but
Could only do so much

Desmos allows you to plot a function and its inverse...first define the function and its domain:

$$f(x)=x^3-6x^2-3\,\{4\le x\}$$

Then define the inverse:

$$x=f(y)$$

[DESMOS=-37.36896540090182,93.61770297027579,-36.842231263227994,8.599804598412113]f\left(x\right)=x^3-6x^2-3\left\{4\le x\right\};x=f\left(y\right)[/DESMOS]

 

[karush]

View attachment 7600

This was my Desmos attempt
But couldn't do the dy/dx