karush
Gold Member
MHB
- 3,240
- 5
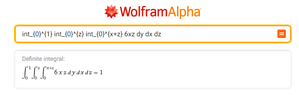
\begin{align}\displaystyle
v_{\tiny{s6.15.6.3}}&=\displaystyle
\int_{0}^{1}\int_{0}^{z}\int_{0}^{x+z}
6xz \quad
\, dy \, dx\, dz
\end{align}
$\text{ok i kinda got ? with $x+z$ to do the first step?}\\$
$\text{didn't see an example}$
v_{\tiny{s6.15.6.3}}&=\displaystyle
\int_{0}^{1}\int_{0}^{z}\int_{0}^{x+z}
6xz \quad
\, dy \, dx\, dz
\end{align}
$\text{ok i kinda got ? with $x+z$ to do the first step?}\\$
$\text{didn't see an example}$