- #1
DrunkenOldFool
- 20
- 0
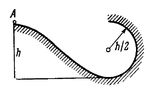
A small body $A$ starts sliding from the height $h$ down an inclined groove passing through into a half circle of radius $h/2$. Assuming friction to be negligiable, find the velocity of the body at the highest point of its trajectory(after breaking off the groove).
View attachment 268
View attachment 268